Реферат: Поиск клик в графах

На основе наблюдений приходим к выводу, что для отыскания клик в неориентированном графе нужно выделить в исходной матрице смежностей подматрицы указанного выше вида, множества вершин образующие эти матрицы и будут вершинами клики. Но по определению клики нам подойдут не все такие множества, а лишь оригинальные не содержащих в себе других множеств вершин. Так что вторая задача будет сводится к выделению из полученных множеств оригинальных, не содержащих в себе других подмножестве. То что исходная матрица смежностей симметрична относительно главной диагонали позволят нам осуществлять поиск подматриц только в ее верхнем или нижнем треугольнике.

Шаг 1.

Идем по матрице как показано на рисунке 3.2 а и ищем первую попавшуюся единичку (рис 3.2 б) запоминаем ее координаты (R,C) .

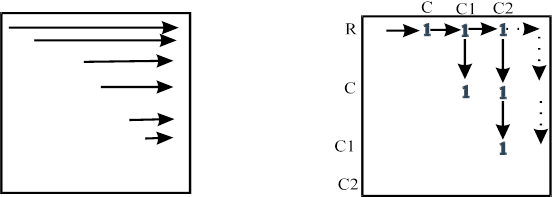
Шаг 2.

Ищем следующую 1 по адресу (R,C1)

Шаг 3.

Начинаем спускаться по столбцу (С1) в поисках 1 , причем ищем ее по адресу (С,С1), так как в исходной матрице столбцы попарно смежных вершин не обязательно соседствуют. Запоминаем строку каждой найденной таким образом 1 для поиска в следующих столбцах. Увеличиваем длину множества вершин на 1.

Количество повторений шага 3 равно текущему размеру множества вершин.

Если по указанному адресу мы не встречаем 1 то значит данный столбец не образует подматрицу смежностей клики - пропускаем его. Начинаем Шаг 2.

Если размер множества вершин образующих клику больше 2 то запоминаем это множество.

Так до конца строки.

Повторяем Шаг 1 для всех 1 в строке.

Таким образом проходим всю матрицу. На выходе получаем несколько множеств вершин, отбираем среди них только оригинальные, не содержащие в себе других подмножеств.

Отобранные подмножества и есть клики заданного графа.

Программная реализация

procedure MakeKliks;

var StolbecSravn,StringSravn,Num,size,i1,i,lenStolb,

Stolbec,RetStolb:byte;

Kstring:klik;

f1:file of byte;

klika:tKlik;

begin

assign(FileKlics,'klics.ots');

rewrite(fileKlics);

assign(f1,'matrica.ots');

reset(f1);

read(f1,size);

for I:=1 to size do