Реферат: Поиск клик в графах

Пусть существует мультиграф с b вершинами, p ребрами, и R компонентами связности, тогда цикломатическое число мультиграфа определяется равенством:

V= p-b+R

Матрицы для графов

Матрицей смежности графа G(X,Гх) , содержащего n вершин называется квадратная бинарная матрица А(G) n x n , c нулями на диагонали. Число единиц в строке равно степени соответствующей вершины.

Матрицей инциденций ориентированного графа G(X,U) называется прямоугольная матрица порядка [m x n] n - мощность множества Х, m - мощность множества U. Каждый элемент которой определяется следующим образом:

1, если х_i - начало дуги U_j

a_ij = -1, если х_i - конец дуги U_j

0, если х_i - не инцидентна дуге U_j

Пример.

Построим матрицы смежности (М1) и инциденций (М2) для графа G(X,U) (рис 2.1).

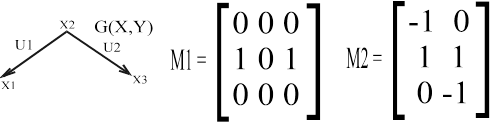
Рис 2.1

Дополнительная матрица графа G(X,U) представляет собой квадратную матрицу А¹ , которая получается из матрицы смежности этого графа путем замены всех нулей единицами и наоборот.

Деревья и прадеревья

Деревом называется неориентированный связный граф с числом вершин не менее двух, не содержащий петель и циклов. Вершины, инцидентные только одной дуге дерева, называются висячими.

Прадрево - ориентированное дерево.

Корень прадерева - вершина у которой Р⁺ (х)=0 .

Глава 2. Максимальные полные подграфы (клики)

Максимальный полный подграф (клика) графа G есть порожденный подграф, построенный на подмножестве S вершин графа и являющийся полным и максимальным в том смысле, что любой другой подграф графа G , построенный на множестве вершин H , содержащих S , не является полным. Следовательно, в клике все вершины попарно смежны. Возможно также определить кликовое число графа (известное также как густота или плотность) - это максимальное число вершин в кликах данного графа.

Часть 2. Практическая реализация курсового проекта

Задание

В неориентированном графе заданном матрицей смежностей выделить клики. Написать программу выполняющую это действие.

Решение

Мой алгоритм нахождения клик в графе

Пусть задан неориентированный граф G1 матрицей смежностей M1 (рис 3.1)

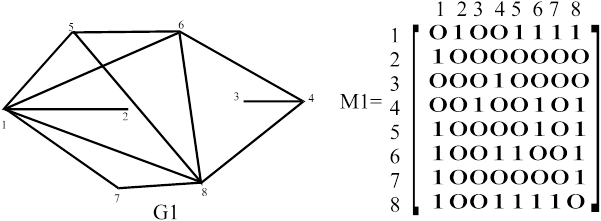Рис 3.1

Замечаем следующее:

1) Что матрица М1 симметрична относительно главной диагонали, так как вершины неориентированного графа попарно смежны.

2) Если выделить клику из данного графа и представить ее в виде матрицы смежностей то получим матрицу вида:

01111 Тоесть тоже симметричную относительно главной диагонали и в верхнем

10111 и нижнем треугольниках ее будут находится 1 а на главной диагонали 0,

11011 так получается потому, что все вершины попарно смежны (см опред.