Реферат: Показатели вариации в статистических исследованиях

Коэффициент вариации является так же количественной мерой однородности совокупности. Принято считать, что если , то совокупность количественно однородна. Чем меньше, тем лучше.

7. Стандартизация данных.

Коэффициенты вариации являются сводными оценками вариаций различных совокупностей. Однако они не позволяют сопоставить между собой значения признака у отдельных или групп единиц разных совокупностей.

Для подобных сравнений прибегают к стандартизации вариантов разных совокупностей по формулам:

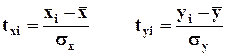, где , - это стандартизированные значения вариантов ряда x и y соответственно. В процессе стандартизации мы переходим от измерения вариантов в натуральных или стоимостных единицах к их измерению величинами соответствующих средне квадратических отклонений.

Пример : Стандартизация данных о доходах на одного члена семьи и среднедушевом потреблении мяса.

Доход на одного члена семьи, тыс. руб./год,	Среднедушевое потребление мяса,
60,7	12,3	-97,5	-25,6	9 506,25	655,36	-1,28	-1,31
84,2	19,1	-74	-18,8	5 476,00	353,44	-0,97	-0,96
112,4	23,1	-45,8	-14,8	2 097,64	219,04	-0,60	-0,76
144,5	35,6	-13,7	-2,3	187,69	5,29	-0,18	-0,12
180,1	49,5	21,9	11,6	479,61	134,56	0,29	0,59
240,9	57,3	82,7	19,4	6 839,29	376,36	1,09	0,99
284,6	68,4	126,4	30,5	15 976,96	930,25	1,66	1,56
1107,4	265,3			40 563,44	2 674,30

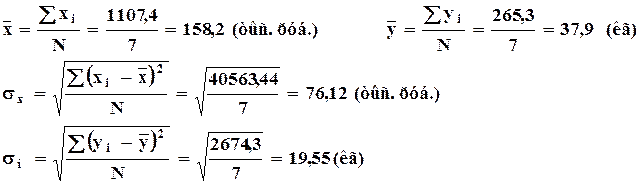
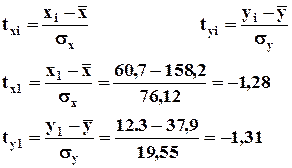
При стандартизации сгруппированных данных наряду с масштабированием вариантов ряда величинами соответствующих средне квадратических отклонений частоты этих рядов пересчитываются в частости.

Стандартизацию данных проводят, когда варианты сравниваемых рядов отличаются единицами измерения и порядком.

Стандартизация является важнейшим статистическим промежуточным этапом.

Стандартизация используется так же хорошо в теории выборочного метода.

8. Моменты распределения.

Моменты распределения составляют алгоритмическую основу многих статистических методов. Различают:

- Произвольные (общий случай);

- Начальные;

- Центральные;

- Стандартные (частный случай).

Выделяют:

- Взвешенные;

- Невзвешенные.

Произвольным моментом k -го порядка называется среднее значение k-ой степени отклонения всех вариантов ряда от произвольного постоянного числа.

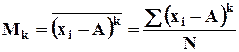- для несгруппированных данных;

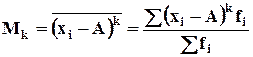- для сгруппированных данных.

При этом k принимает целочисленное значение от 1 до 4.

Если А=0 , то произвольный момент преобразуется в начальный момент .

- для несгруппированных данных;

при k=1 M₁ =

при k=2 M₂ =