Реферат: Показатели вариации в статистических исследованиях

1. Понятие вариации и роль ее изучения в статистических исследованиях.

2. Измерители вариации.

3. Прямой способ расчета показателей вариации.

4. Свойства дисперсии и среднего квадратического отклонения.

5. Упрощенный способ расчета дисперсии и средне квадратического отклонения.

6. Относительные показатели вариации.

7. Стандартизация данных.

8. Моменты распределения.

9. Показатели асимметрии и эксцесса.

10. Средняя арифметическая и дисперсия альтернативного признака.

1. Понятие вариации и роль ее изучения в статистических исследованиях.

Вариация – это колеблемость значений признака у отдельных единиц совокупности.

Наличию вариации обязана своим появлением статистика. Большинство статистических закономерностей проявляется через вариацию. Изучая вариацию значений признака в сочетании с его частотными характеристиками, мы обнаруживаем закономерности распределения (например: население по возрасту, студентов по уровню оценок).

Рассматривая вариацию одного признака параллельно с изменением другого, мы обнаруживаем взаимосвязи между этими признаками или их отсутствие (например: зависимость между торговой площадью и товарооборотом).

Вариации в статистике проявляются двояко, либо через изменения значений признака у отдельных единиц совокупности, либо через наличие или отсутствие изучаемого признака у отдельных единиц совокупности.

Изучение вариации в статистике имеет как самостоятельную цель, так и является промежуточным этапом более сложных статистических исследований.

2. Измерители вариации.

Простейшим показателем вариации является размах колебаний : .

Достоинство этого показателя простота расчета, возможность использования для оценки вариации однородных совокупностей. Недостаток – неприемлемость для неоднородных совокупностей с редкими выбросами крайних значений признака.

Частично недостатки этого показателя устраняет межквартельный размах : . Однако, он характеризует вариацию только половины совокупности.

Для учета колеблемости всех значений признака применяют показатели среднего линейного отклонения, дисперсии и средне квадратического отклонения.

Средне линейное отклонение – среднее значение отклонений всех вариантов ряда от средней арифметической (иногда от моды или медианы):

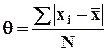- для несгруппированных данных;

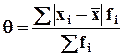- для сгруппированных данных.

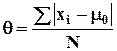
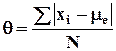
Аналогичным по смыслу среднему линейному отклонению является показатель дисперсии и рассчитываемый на его основе показатель средне квадратического отклонения.

Дисперсия – рассеивание, данный показатель характеризует рассеивание значений признака относительно его средней величины.

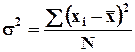- для несгруппированных данных;

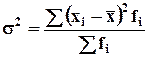- для сгруппированных данных.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--