Реферат: Полупроводники 2

С ростом температуры концентрация дырок возрастает и может стать сравнимой с концентрацией электронов, тогда уравнение электронейтральности будет иметь вид: .

Решая это уравнение, получим

.

Учитывая связь между n и F и предыдущую формулу, то можно записать выражение для уровня Ферми в области высоких температур:

.

По мере приближения уровня Ферми к середине запрещенной зоны концентрация дырок возрастает при практически неизменной концентрации электронов. При дальнейшем росте концентрации дырок будет происходить и рост концентрации электронов, достигается равенство n=p, и полупроводник из примесного превращается в собственный. Температура, при которой происходит этот переход, называется температурой истощения примеси.

Условием перехода будет выступать равенство p = N_D или n =2 N_D , откуда можно найти эту граничную температуру:

,

или

.

Концентрация, при которой наступает полное вырождение полупроводника (), находится из соотношения:

и будет равна

.

Вывод формул для дырочного полупроводника аналогичен выводу для электронного.

Основные формулы для дырочного полупроводника:

Зависимость концентрации дырок от температуры в области низких температур:

Зависимость уровня Ферми от температуры в области низких температур:

Зависимость концентрации дырок от температуры в области высоких температур:

Зависимость уровня Ферми от температуры в области высоких температур:

Температура насыщения примеси:

Температура истощения примеси:

Концентрация акцепторов, при которой наступает полное вырождение:

.

Расчет времени жизни носителей заряда.

Реальные полупроводниковые материалы содержат обычно примеси нескольких типов, каждая из которых может создавать один или несколько уровней в запрещенной зоне полупроводника. Дефекты решетки, обычно нейтральные в состоянии термодинамического равновесия и способные захватывать подвижные носители заряда одного знака и освобождать их, называются ловушками захвата. Ограничимся рассмотрением случая, когда в полупроводнике имеется один тип ловушек, создающий энергетический уровень.

Время жизни носителей заряда определяется формулой

.

В случае малого уровня возбуждения, когда , время жизни неравновесных носителей заряда имеет вид:

,

,,

где Sp и Sn – сечения захвата электронов и дырок,

Nt – концентрация рекомбинационных центров,

V_T – тепловая скорость.

Расчет s ( T ). Формулы для подвижности.

Удельная электропроводность примесных полупроводников определяется по формуле s= qn m _n для донорного и по формуле s= qp m _p для акцепторнрго полупроводника. Для вычисления s (T)необходимо найти температурную зависимость подвижности.

Кремний является неполярным полупроводником. Для него существуют два основных механизма рассеяния, которые существенно влияют на подвижность, а именно рассеяние на акустических фононах и на ионизированных примесях.

При низких температурах, когда число фононов в кристалле сильно уменьшено охлаждением, подвижность определяется рассеянием на ионизованных примесных центрах.

Каждый ионизованный центр в кристалле представляет собой неподвижный отрицательный или положительный заряд, который может отклонить траекторию пролетающего электрона.

Подвижность, связанная с рассеянием на ионах примеси, описывается формулой Бруккса-Херринга:

,

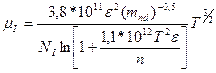где N_I – концентрация ионов примеси, n – концентрация электронов проводимости.

При высоких температурах в Si электроны рассеиваются преимущественно продольными акустическими фононами.

При возникновении продольных акустических колебаний происходит смещение центра тяжести элементарной ячейки и происходит упругая деформация кристаллической решетки, которая приводит к изменению положения краев зоны проводимости и валентной зоны, что адекватно возникновению на пути движения носителей заряда потонциального барьера и рассеянию на нем носителей заряда.