Реферат: Помехи и их классификация. Задача обнаружения и методика ее решения

БЕЛОРУССКИЙ ГОСУДРАСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра ЭТТ

РЕФЕРАТ

На тему:

"Помехи и их классификация. Задача обнаружения и методика ее решения"

МИНСК, 2008

Помехи и их классификация.

Решение всех задач (обнаружение, распознавание-различение, измерение параметров сигнала) всегда затрудняется наличием помех искусственного или естественного происхождения. С точки зрения характера воздействия помех на работу систем и принципов их защиты помехи целесообразно разделить на группы: шумы, мешающие излучения и мешающие отражения. Как и сигналы, помехи являются электромагнитными полями и характеризуются пространственной, поляризационной и временной структурой. Однако, как и в случае с сигналами сосредоточим внимание только на их временной структуре.

Внутренние шумы приемных устройств, а также внешние активные шумовые помехи, преднамеренно создаваемые для противодействия работе РТС, имеют подобные временные структуры и поэтому рассматриваются объединение.

Шум (мешающие излучения) представляет собой нормальный случайный процесс с флуктуирующей амплитудой и фазой:

h(t) = H(t) exp(iω0t) = xh(t) + iyh(t),

где H(t) - комплексная огибающая шума

xh(t), yh(t) - квадратурные составляющие шума.

Одна из квадратурных составляющих шума показана на рис.1 Корреляционная функция шума является результатом статистического усреднения

где σш2 - средняя мощность шума,

rш(τ) - нормированная корреляционная функция шума.

Заметим, что средние значения шума, его комплексной огибавшей и квадратурных составляющих равны нулю:

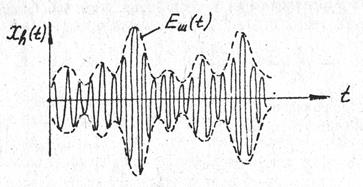
Рис.1. Одна из квадратурных составляющих шума.

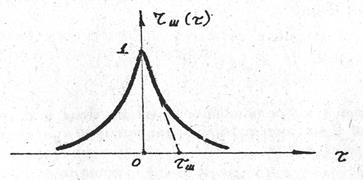
Рис.2. Нормированная корреляционная функция шума.

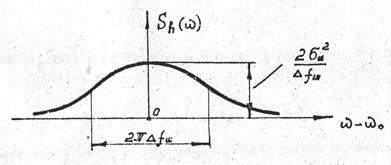
Рис.3. Энергетический спектр шума.

Нормированная корреляционная функция шума чаще всего аппроксимируется экспонентой (рис.2):

где τш - время корреляции шума.

Энергетический спектр шума

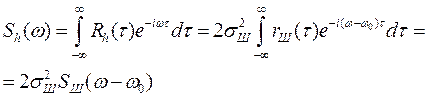
--> ЧИТАТЬ ПОЛНОСТЬЮ <--