Реферат: Построение эйлерова цикла. Алгоритм Форда и Уоршелла
Предположим, что уже построена простая цепь mk -1 = {e 1 , e 2 , …, ek -1 } для k ³2 методом, указанным в алгоритме. Пусть ek -1 = (xk -2 , xk -1 ) и xk -1 ¹a . Рассмотрим подграф ![]() , который получается из подграфа G k -1 (X , E\ mk -1 ) удалением всех изолированных вершин. Вершина xk -1 в этом подграфе
, который получается из подграфа G k -1 (X , E\ mk -1 ) удалением всех изолированных вершин. Вершина xk -1 в этом подграфе ![]() имеет нечетную степень, поэтому существует по крайней мере одно ребро ek ÎE\ mk -1 , инцидентное xk -1 . Если это ребро единственное, то оно не является мостом в графе
имеет нечетную степень, поэтому существует по крайней мере одно ребро ek ÎE\ mk -1 , инцидентное xk -1 . Если это ребро единственное, то оно не является мостом в графе ![]() . В противном случае вершина a будет связана с некоторой вершиной
. В противном случае вершина a будет связана с некоторой вершиной ![]() единственной цепью, содержащей ребро ek , что противоречит существованию эйлерова цикла в графе G . Поскольку ek - не мост, то процесс можно продолжать, взяв
единственной цепью, содержащей ребро ek , что противоречит существованию эйлерова цикла в графе G . Поскольку ek - не мост, то процесс можно продолжать, взяв ![]() . Если ребро ek не единственное инцидентное вершине xk -1 , то среди этих ребер есть по крайней мере одно, не являющееся мостом. В противном случае один из этих мостов
. Если ребро ek не единственное инцидентное вершине xk -1 , то среди этих ребер есть по крайней мере одно, не являющееся мостом. В противном случае один из этих мостов ![]() можно выбросить так, что вершины xk -1 и a попадут в разные компоненты связности графа
можно выбросить так, что вершины xk -1 и a попадут в разные компоненты связности графа ![]() . Если xk -1 принадлежит компоненте M , то в этой компоненте все вершины имеют четную степень, поэтому существует эйлеров цикл в M , проходящий через xk -1 . Этот цикл содержит все ребра, инцидентные xk -1 и принадлежащие
. Если xk -1 принадлежит компоненте M , то в этой компоненте все вершины имеют четную степень, поэтому существует эйлеров цикл в M , проходящий через xk -1 . Этот цикл содержит все ребра, инцидентные xk -1 и принадлежащие ![]() , являющиеся одновременно мостами. Получено противоречие, так как ребра из эйлерова цикла мостами быть не могут. Итак, в рассмотренном случае существует ребро ek , инцидентное вершине xk -1 и не являющееся мостом. Значит, и в этом случае процесс можно продолжать, взяв
, являющиеся одновременно мостами. Получено противоречие, так как ребра из эйлерова цикла мостами быть не могут. Итак, в рассмотренном случае существует ребро ek , инцидентное вершине xk -1 и не являющееся мостом. Значит, и в этом случае процесс можно продолжать, взяв
![]() .
.
Из предыдущего следует, что процесс нельзя продолжать тогда и только тогда, когда мы попадем в вершину a , причем степень вершины a относительно непройденных ребер равна нулю. Докажем, что в этом случае построенный цикл m - простой цикл. Покажем, что m содержит все ребра графа G . Если не все ребра графа G принадлежат m, то не принадлежащие m ребра порождают компоненты связности C 1 , …, Cm (m ³1) в подграфе ![]() . Пусть компонента Ci , 1£i £m соединяется с циклом m в вершине yi . Если существует ребро e Îm , такое, что e =(yi , a ), то при построении цикла m было нарушено правило выбора ребра e , что невозможно. Если часть цикла m, соединяющая yi и a , состоит более чем из одного ребра, то первое ребро этой части
. Пусть компонента Ci , 1£i £m соединяется с циклом m в вершине yi . Если существует ребро e Îm , такое, что e =(yi , a ), то при построении цикла m было нарушено правило выбора ребра e , что невозможно. Если часть цикла m, соединяющая yi и a , состоит более чем из одного ребра, то первое ребро этой части ![]() было мостом, и поэтому было нарушено правило выбора
было мостом, и поэтому было нарушено правило выбора ![]() , что невозможно. Итак, непройденных ребер быть не может, поэтому m - эйлеров цикл.
, что невозможно. Итак, непройденных ребер быть не может, поэтому m - эйлеров цикл.
2. НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ
Рассматрим ориентированные графы G (X , E ) каждой дуге e ÎE которого ставится в соответствие вещественное число l (e ). Т.е. на множестве Е создана функция l :E ®R . Такой граф принято называть нагруженным . Само число l называется весом дуги.
Можно увидеть аналогию между, например, картой автомобильных или железных дорог. Тогда множество вершин Х будет соответствовать городам, множество дуг – магистралям, соединяющим города, а веса – расстояниям. (На практике, при этом, фактически получится неориентированный граф).
В связи с изложенной аналогией будем называть веса дуг расстояниями.
Определение 2. 1. Пусть имеется последовательность вершин x 0 , x 1 , …, xn , которая определяет путь в нагруженном графе G (X , E ), тогда длина этого пути определяется как  .
.
Естественный интерес представляет нахождение кратчайшего пути между двумя заданными вершинами x и y.
Алгоритм Форда отыскания кратчайшего пути .
Будем предполагать, что все расстояния в графе положительны. (Если это не так, то ко всем весам можно всегда добавить такую константу, что все эти веса станут положительными).
Пусть мы ищем путь от вершины x 0 к вершине xn . Будем каждой вершине xi ставить в соответствие некоторое число li по следующим правилам.
1° Положим l0 = 0, li = ¥ (достаточно большое число) для "i > 0.
2° Ищем в графе дугу (xi , xj ) удовлетворяющую следующему условию
lj - li > l (xi , xj ), (1)
после чего заменяем lj на
![]() .
.
Пункт 2°повторяется до тех пор, пока невозможно будет найти дугу, удовлетворяющую условию (1). Обоснуем этот алгоритм и укажем как определяется кратчайший путь.
Отметим, что ln монотонно уменьшается, то после завершения алгоритма найдется дуга ![]() , такая, что
, такая, что ![]() для которой последний раз уменьшалось ln . (Иначе вообще нет пути между x 0 и xn или для
для которой последний раз уменьшалось ln . (Иначе вообще нет пути между x 0 и xn или для ![]() верно (1)).
верно (1)).
По этой же самой причине найдется вершина ![]() , такая , что
, такая , что
![]() ,
,
этот процесс может продолжаться и дальше, так что получится строго убывающая последовательность ![]() . Отсюда следует, что при некотором k мы получим
. Отсюда следует, что при некотором k мы получим ![]() .
.
Покажем, что ![]() – минимальный путь с длиной ln , т.е. длина любого другого пути между x 0 и xn не превышает kn .
– минимальный путь с длиной ln , т.е. длина любого другого пути между x 0 и xn не превышает kn .
Возьмем произвольный путь ![]() и рассмотрим его длину
и рассмотрим его длину ![]() .
.
После завершения алгоритма имеем следующие соотношения
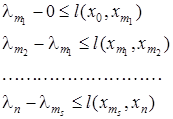
Сложив все эти неравенства, получим
![]() ,
,
что и требовалось доказать.