Реферат: Построение эйлерова цикла. Алгоритм Форда и Уоршелла
4°. Выписать кратчайший путь между ![]() и xj .
и xj .
Пункты 3° и 4° предполагают рекурсивное обращение к рассмотренному алгоритму.
С задачей определения кратчайших путей в графе тесно связана задача транзитивного замыкания бинарного отношения.
Напомним, что бинарным отношением на множестве Х называется произвольное подмножество E ÌX ´X .
Транзитивным называется отношение, удовлетворяющее следующему условию: если (x , y ) ÎE и (y , z ) ÎE , то (x , z ) ÎE для всех x , y , z ÎX . Отметим, что бинарное отношение можно однозначно представить орграфом G (X , E ). Теперь для произвольного отношения Е определим новое отношение Е * следующим образом
E * = {(x , y ) | если в G (X , E ) существует путь ненулевой длины из x в y }.
Легко проверить, что Е * - транзитивное отношение. Кроме того, Е * является наименьшим транзитивным отношением на Х в том смысле, что для произвольного транзитивного отношения F ÉE выполняется E * ÉF . Отношение Е * называется транзитивным замыканием отношения Е .
Если отношение Е представить в виде графа G (X , E ) в котором каждая дуга имеет вес 1, то транзитивное замыкание Е * можно вычислить с помощью алгоритма Флойда. При этом надо учесть, что
(xi , xj ) ÎE * если ![]() .
.
Для большего удобства алгоритм Флойда в этом случае можно модифицировать следующим образом.
Положим
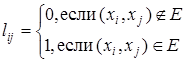 .
.
Вместо (3) запишем
![]() ,
,
где Ú – дизъюнкция (логическое сложение),
Ù – конъюнкция (логическое умножение).
После завершения работы алгоритма будем иметь
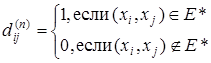
Модифицированный таким образом алгоритм называется алгоритмом Уоршелла.
ЛИТЕРАТУРА
1. Баканович Э.А., Волорова Н.А., Епихин А.В. Дискретная математика:. В 2-х ч..– Мн.: БГУИР, 2000.– 52 с., ил. 14 ISBN 985-444-057-5 (ч. 2).
2. Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации. М. Иза-во МГТУ им. Н.Э.Баумана, 2003.
3. Белоусов А.И., Ткачев С.Б. Дискретная математика: Учебник для ВУЗов / Под ред. В.С. Зарубина, А.П. Крищенко.– М.: изд-во МГТУ им. Н.Э. Баумана, 2001.– 744 с. (Сер. Математика в техническом университете; Вып XIX).