Реферат: Построение эйлерова цикла. Алгоритм Форда и Уоршелла

а б

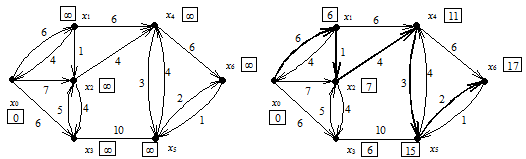
Рис. 2.1

На рис. 2.1а изображен исходный помеченный граф и начальные значения l_i . На рис. 2.1б для того же графа указаны конечные значения l_i и выделен кратчайший путь. Пометка вершин графа происходила в следующем порядке (в скобках указана дуга, вдоль которой выполняется (1)):

l₁ = 6 (x ₀ , x ₁ ),

l₂ = 7 (x ₀ , x ₂ ),

l₃ = 6 (x ₀ , x ₃ ),

l₄ = 12 (x ₁ , x ₃ ),

l₄ = 11 (x ₂ , x ₄ ),

l₅ = 16 (x ₃ , x ₄ ),

l₅ = 15 (x ₄ , x ₅ ),

l₆ = 18 (x ₄ , x ₆ ),

l₆ = 17 (x ₅ , x ₆ ).

Иногда возникает задача отыскания кратчайших расстояний между всеми парами вершин. Одним из способов решения этой задачи является

Алгоритм Флойда

Обозначим l_ij длину дуги (x_i , x_j ), если таковой не существует примем l_ij = ¥, кроме того, положим l_ii = 0. Обозначим длину кратчайшего из путей из x_i в x_j с промежуточными вершинами из множества {x ₁ , …, x_m }. Тогда можно получить следующие уравнения

, (2)

. (3)

Уравнение (2) очевидно. Обоснуем уравнение (3). Рассмотрим кратчай­ший путь из x_i в x_j с промежуточными вершинами из множества {x ₁ , …, x_m , x_{m +1} }. Если этот путь не содержит x_{m +1} , то . Если же он содержит x_{m +1} , то деля путь на отрезки от x_i до x_{m +1} и от x_{m +1} до x_j , получаем равенство .

Уравнения (2) и (3) позволяют легко вычислить матрицу расстояний [d_ij ] между всеми парами вершин графа G (X , E ). На первом этапе согласно (2) составляем n ´n матрицу равную матрице [l_ij ] весов ребер (n – число вершин G (X , E )). n раз производим вычисление по итерационной формуле (3), после чего имеем – матрицу расстояний.

Отметим, что алгоритм Флойда непосредственно не указывает сам кратчайший путь между вершинами, а только его длину. Алгоритм Флойда можно модифицировать таким образом, чтобы можно было находить и сами пути. Для этого получим вспомогательную матрицу [R_ij ], которая будет содержать наибольший номер вершины некоторого кратчайшего пути из x_i в x_j (R_ij =0, если этот путь не содержит промежуточных вершин).

Эта матрица вычисляется параллельно с по следующим правилам

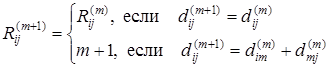
Последнее выражение следует из обоснования (3).

Теперь кратчайший путь выписывается из следующего рекурсивного алгоритма:

Кратчайший путь из x_i в x_j :

1°. Если R_ij = 0 то выполнить 2°,

иначе выполнить 3°.

2°. Если i =j то выписать x_i и закончить,

иначе выписать x_i и x_j закончить.