Реферат: Построение и графическое изображение вариационных рядов
Составление вариационных рядов рассмотрим на примере данных о бонитете почв и урожайности овощей (Таблица исходных данных). Они являются исходными данными для демонстрационного примера.
Дискретный вариационный ряд строится по зависимому признаку (обозначим его У), интервальный - по независимому (Х).
Для того чтобы составить дискретный вариационный ряд урожайности овощей, необходимо расположить наблюдавшиеся значения признака в порядке возрастания, т.е. ранжирование статистических данных, а затем подсчитать частоты (сколько раз встречается то или иное значение признака).
Для графического изображения дискретного ряда служит многоугольник (полигон). При его построении на оси абсцисс откладываются варианты, на оси ординат - частоты.
Построение интервального вариационного ряда рассматривается на примере бонитета почв различных хозяйств.
Для этого:
1 . Определим число групп (число интервалов) по формуле Стерджесса:
K=1+3.32*lg (n),
где:
К-число групп (интервалов);
n- число единиц наблюдения.
В данном примере K=1+3.32*lg(30) = 6.
2. Рассчитываем величину интервала, т.е. разность между верхним и нижним значением признака в группе: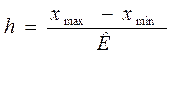 
Величина интервала (шаг):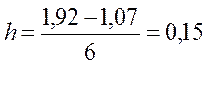 
3. Формируем группы, т.е. устанавливаем верхние и нижние границы для каждого интервала. Нижней границей для первой группы будет xmin (или эта величина, уменьшенная не более чем на половину величины интервала). Чтобы найти верхнюю границу, нужно к нижней границе прибавить величину интервала h.
Верхняя граница первой группы будет нижней границей для второго интервала. Чтобы найти верхнюю границу, к полученному значению опять прибавляют величину интервала и т.д.
4. Подсчитываем число вариант, попавших в каждый интервал, Варианты, совпадающие с границами частичных интервалов, включаются в правый интервал. Графически интервальный ряд изображают с помощью гистограммы.
Глава 2. Статистические характеристики рядов распределения.
2.1. Показатели центра распределения .
Средней в статистике называется показатель, характеризующий типичный размер признака в совокупности.
Средняя арифметическая вычисляется по формулам:
простая 
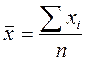; взвешенная 
,
где 
- среднее значение признака; 
- варианты; 
- частоты; 
- численность совокупности.
Характеристиками вариационных рядов наряду со степенными средними являются мода и медиана.
Мода - величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. В дискретных рядах распределения модой будет варианта с наибольшей частотой.
В интервальном ряду мода определя6ется по формуле:
,
где 
-нижняя граница интервала, содержащего моду; 
- величина модального интервала; 
- частота модального интервала; 
- частота интервала, предшествующего модальному; 
- частота послемодального интервала.
Медианой в статистике называется варианта, расположенная в середине вариационного ряда. Если ряд дискретный имеет нечётное число, то медианой будет варианта, расположенная в середине упорядоченного ряда и её порядковый номер
. Если ряд состоит из чётного числа членов, то медианой будет средняя арифметическая из двух вариант в середине ряда с порядковыми номерами: 
и 
.
В интервальном ряду медиана рассчитывается по формуле:
