Реферат: Построение и графическое изображение вариационных рядов
Ух = 58,964х2 -88,707х+112,8
Для оценки степени пригодности полученного корреляционного уравнения в практических целях необходимо проверить его достоверность.
Рассчитываем ошибку уравнения по формуле:
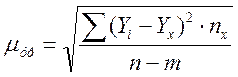
где Yi - фактическое значение результативного признака, в демонстрационном примере – это Уфакт.; Yх - значения результативного признака, рассчитанные по уравнению регрессии, в демонстрационном примере – это Урасчетн.; n –число наблюдений, m- число параметров уравнения регрессии.
Значения Yх рассчитываются по уравнению регрессии путем подставления в него значений фактического признака (х). В РГР необходимо подсчитать ошибку уравнения для всех видов зависимостей, найти относительную ошибку уравнения, а также выявить минимальную ошибку уравнения регрессии, и убедиться, что она соответствует той зависимости, у которой самый высокий коэффициент аппроксимации (R2 ).
Минимальная ошибка уравнения равна 5,308431. Она соответствует линейной зависимости, у которой самый высокий коэффициент аппроксимации (R2 ), равный 0,8572.
Глава 4. Дисперсионный анализ.
4.1. Понятие дисперсионного анализа
В основе дисперсионного анализа лежит правило сложения дисперсий. В соответствии с ним общая дисперсия результативного признака при сгруппированных данных равна сумме межгрупповой и внутригрупповой дисперсий.
Межгрупповая вариация результативного признака вызвана влиянием на него одного или нескольких изучаемых факторных признаков. Дисперсию, измеряющую межгрупповую вариацию, называют межгрупповой или факторной. Внутригрупповая вариация является результатом влияния на результативный признак неучтенных факторов. Показатель, характеризующий внутригрупповую вариацию, называется внутригрупповой или остаточной дисперсией. Весь объём вариации результативного признака характеризуется общей дисперсией.
Идея дисперсионного анализа заключается в сравнении факторной дисперсии с остаточной. Отношение факторной дисперсии к остаточной носит название F- критерия или критерия Фишера и используется для оценки достоверности связи между результативным и факторными признаками. Если различие между факторной и остаточной дисперсиями значимо, то делается вывод о том, что фактор оказывает существенное влияние на результативный признак
Список литературы
1. Венецкий И.Г., Кильдишев В.С. Теория вероятностей и математическая статистика. М.: Статистика, 1975.
2. Ефимова М.Р., Рябцев В.М. Общая теория статистики. М.: Финансы и статистика, 1991.
3. Марк Джон, Крейг Стинсон. Эффективная работа с MicrosoftExcel 2000. СПб.: Питер 2001.
4. Блаттнер Патрик. Использование MicrosoftExcel 2002. М.: Издательский дом «Вильямс», 2002.
Приложение 1.
Значение дифференциальной функции Лапласа
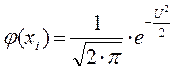
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 | 0,3989 | ,3989 | ,3989 | ,3988 | ,3986 | ,3984 | ,3982 | ,3980 | ,3977 | ,3973 |
| 0,1 | ,3970 | ,3965 | ,3961 | ,3956 | ,3951 | ,3945 | ,3939 | ,3932 | ,3925 | ,3918 |
| 0,2 | ,3910 | ,3902 | ,3894 | ,3885 | ,3846 | ,3857 | ,3857 | ,3847 | ,3836 | ,3825 |
| 0,3 | ,3814 | ,3802 | ,3790 | ,3778 | ,3765 | ,3752 | ,3739 | ,3726 | ,3712 | ,3697 |
| 0,4 | ,3683 | ,3668 | ,3652 | ,3637 | ,3621 | ,3605 | ,3589 | ,3572 | ,3555 | ,3538 |
| 0,5 | ,3521 | ,3503 | ,3485 | ,3467 | ,3448 | ,3429 | ,3410 | ,3391 | ,3372 | ,3352 |
| 0,6 | ,3332 | ,3312 | ,3292 | ,3271 | ,3251 | ,3230 | ,3209 | ,3187 | ,3166 | ,3134 |
| 0,7 | ,3123 | ,3101 | ,3079 | ,3056 | ,3054 | ,3011 | ,2989 | ,2966 | ,2973 | ,2920 |
| 0,8 | ,2897 | ,2874 | ,2850 | ,2827 | ,2803 | ,2780 | ,2756 | ,2732 | ,2709 | ,2685 |
| 0,9 | ,2661 | ,2637 | ,2613 | ,2589 | ,2565 | ,2541 | ,2516 | ,2492 | ,2468 | ,2443 |
| 1,0 | ,2420 | ,2396 | ,2371 | ,2347 | ,2323 | ,2299 | ,2275 | ,2251 | ,2227 | ,2203 |
| 1,1 | ,2179 | ,2155 | ,2131 | ,2107 | ,2083 | ,2059 | ,2036 | ,2012 | ,1989 | ,1965 |
| 1,2 | ,1942 | ,1919 | ,1895 | ,1872 | ,1849 | ,1826 | ,1804 | ,1781 | ,1758 | ,1736 |
| 1,3 | ,1714 | ,1691 | ,1696 | ,1647 | ,1626 | ,1604 | ,1582 | ,1561 | ,1539 | ,1518 |
| 1,4 | ,1497 | ,1476 | ,1456 | ,1435 | ,1415 | ,1394 | ,1374 | ,1354 | ,1334 | ,1315 |
| 1,5 | ,1295 | ,1276 | ,1267 | ,1238 | ,1219 | ,1200 | ,1182 | ,1163 | ,1145 | ,1127 |
| 1,6 | ,1109 | ,1092 | ,1074 | ,1057 | ,1040 | ,1023 | ,1006 | ,0989 | ,0973 | ,0957 |
| 1,7 | ,0940 | ,0925 | ,0909 | ,0893 | ,0878 | ,0863 | ,0848 | ,0843 | ,0818 | ,0804 |
| 1,8 | ,0790 | ,0775 | ,0761 | ,0748 | ,0734 | ,0721 | ,0707 | ,0694 | ,0681 | ,0669 |
| 1,9 | ,0658 | ,0644 | ,0632 | ,0620 | ,0608 | ,0596 | ,0584 | ,0573 | ,0562 | ,0551 |
| 2,0 | ,0540 | ,0529 | ,0519 | ,0508 | ,0498 | ,0488 | ,0478 | ,0468 | ,0459 | ,0449 |
| 2,1 | ,0440 | ,0431 | ,0422 | ,0413 | ,0404 | ,0396 | ,0387 | ,0379 | ,0371 | ,0363 |
| 2,2 | ,0355 | ,0347 | ,0339 | ,0332 | ,0325 | ,0317 | ,0310 | ,0303 | ,0227 | ,0290 |
| 2,3 | ,0283 | ,0277 | ,0270 | ,0264 | ,0258 | ,0252 | ,0246 | ,0241 | ,0235 | ,0229 |
| 2,4 | ,0224 | ,0219 | ,0213 | ,0208 | ,0203 | ,0198 | ,0194 | ,0189 | ,0184 | ,0180 |
| 2,5 | ,0173 | ,0171 | ,0167 | ,0163 | ,0158 | ,0154 | ,0151 | ,0147 | ,0143 | ,0139 |
| 2,6 | ,0136 | ,0132 | ,0129 | ,0126 | ,0122 | ,,0119 | ,0116 | ,0113 | ,0110 | ,0107 |
| 2,7 | ,0104 | ,0101 | ,0098 | ,0096 | ,0093 | ,0091 | ,0088 | ,0086 | ,0084 | ,0081 |
| 2,8 | ,0079 | ,0077 | ,0075 | ,0073 | ,0071 | ,0069 | ,0067 | ,0065 | ,0063 | ,0061 |
| 2,9 | ,0060 | ,0058 | ,0056 | ,0055 | ,0053 | ,0051 | ,0050 | ,0048 | ,0047 | ,0046 |
| 3,0 | ,0044 | ,0043 | ,0042 | ,0040 | ,0039 | ,0038 | ,0037 | ,0036 | ,0035 | ,0034 |
| 3,1 | ,0033 | ,0032 | ,0031 | ,0030 | ,0029 | ,0028 | ,0027 | ,0026 | ,0025 | ,0025 |
| 3,2 | ,0024 | ,0023 | ,0022 | ,0022 | ,0021 | ,0020 | ,0020 | ,0019 | ,0018 | ,0018 |
| 3,3 | ,0017 | ,0017 | ,0016 | ,0016 | ,0015 | ,0015 | ,0014 | ,0014 | ,0013 | ,0013 |
| 3,4 | ,0012 | ,0012 | ,0012 | ,0011 | ,0011 | ,0010 | ,0010 | ,0010 | ,0009 | ,0009 |
| 3,5 | ,0009 | ,0008 | ,0008 | ,0008 | ,0008 | ,0007 | ,0007 | ,0007 | ,0007 | ,0006 |
| 3,6 | ,0006 | ,0006 | ,0006 | ,0005 | ,0005 | ,0005 | ,0005 | ,0005 | ,0005 | ,0004 |
| 3,7 | ,0004 | ,0004 | ,0004 | ,0004 | ,0004 | ,0004 | ,0003 | ,0003 | ,0003 | ,0003 |
| 3,8 | ,0003 | ,0003 | ,0003 | ,0003 | ,0003 | ,0002 | ,0002 | ,0002 | ,0002 | ,0002 |
| 3,9 | ,0002 | ,0002 | ,0002 | ,0002 | ,0002 | ,0002 | ,0002 | ,0002 | ,0001 | ,0001 |
Приложение 2.
Критические точки распределения x 2
Уровень Значимости, α | Число степеней свободы, к | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 0,01 | 6,6 | 9,2 | 11,3 | 13,3 | 15,1 | 16,8 | 18,5 | 20,1 | 21,7 | 23,2 | 24,7 | 26,2 | 27,7 | 29,1 | 30,6 |
| 0,05 | 3,8 | 6,0 | 7,8 | 9,9 | 11,1 | 12,6 | 14,1 | 15,5 | 16,9 | 18,3 | 19,7 | 21,0 | 22,4 | 23,7 | 25,0 |
Приложение 3.
Критические точки распределения Стьюдента
Число степеней свободы, к | Уровень значимости, α (двусторонняя критическая область) | Число степеней свободы к | Уровень значимости, α (двусторонняя критическая область) | ||
| 0,05 | 0,01 | 0,05 | 0,01 | ||
| 1 | 12,7 | 63,7 | 18 | 2,10 | 2,88 |
| 2 | 4,30 | 9,92 | 19 | 2,09 | 2,86 |
| 3 | 3,18 | 5,84 | 20 | 2,09 | 2,85 |
| 4 | 2,78 | 4,60 | 21 | 2,08 | 2,83 |
| 5 | 2,57 | 4,03 | 22 | 2,07 | 2,82 |
| 6 | 2,45 | 3,71 | 23 | 2,07 | 2,81 |
| 7 | 2,36 | 3,50 | 24 | 2,06 | 2,80 |
| 8 | 2,31 | 3,36 | 25 | 2,06 | 2,79 |
| 9 | 2,26 | 3,25 | 26 | 2,06 | 2,78 |
| 10 | 2,23 | 3,17 | 27 | 2,05 | 2,77 |
| 11 | 2,20 | 3,11 | 28 | 2,05 | 2,76 |
| 12 | 2,18 | 3,05 | 29 | 2,05 | 2,76 |
| 13 | 2,16 | 3,01 | 30 | 2,04 | 2,75 |
| 14 | 2,14 | 2,98 | 40 | 2,02 | 2,70 |
| 15 | 2,13 | 2,95 | 60 | 2,00 | 2,66 |
| 16 | 2,12 | 2,92 | 120 | 1,98 | 2,62 |
| 17 | 2,11 | 2,90 | - | 1,96 | 2,58 |
| 2,025 | 0,005 | ||||
| Уровень значимости α (односторонняя критическая область) | |||||