Реферат: Построение и исследование динамической модели портального манипулятора
причем 
, 
и 
.
Решение системы (2.7) имеет вид:
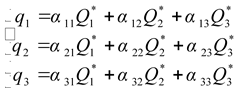 , | (2.8) |
где
 | (2.9) |
.
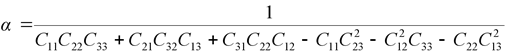На систему действуют обобщенные силы, которыми являются инерционные силы и силы сопротивления движению. Обычно в сложных системах в целях упрощения [4, 5] силу сопротивления принимают пропорциональной первой степени скорости движения. С целью упрощения условимся, что угол 
мал и координаты массы m можно записать как 
. Поэтому на основании кинетостатики можем записать:
 , | (2.10) |
где 
- обобщенная сила, 
- коэффициент сопротивления пропорциональный первой степени скорости движения массы m . Так как масса собственно консоли манипулятора МРЛ-901П меньше массы закрепленных на ней рабочих головок, захватов и деталей, для упрощения примем условие, что точка исследования колебаний (практически - рабочий орган манипулятора) совпадает с точкой приложения сосредоточенной массы m .
Сила 
действует на все звенья манипулятора следовательно:
 | (2.11) |
Коэффициенты 
в (2.7) будем определять из того, что согласно (2.11) звенья можно рассматривать независимо друг от друга. Положим сначала, что 
действует только по координате 
, затем только по координате 
и наконец только по координате 
, тогда в выражение (2.7) можно переписать:
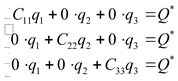 , | (2.12) |
таким образом 
, используя (2.9) находим:
 | (2.13) |
Коэффициенты 
, 
и 
определяют податливость звеньев манипулятора по координатам 
, 
и 
соответственно. Выражая податливость звеньев через их жесткость, запишем:
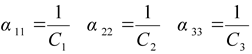 , | (2.14) |
где 
, 
и 
жесткости звеньев по координатам 
, 
и соответственно.
Подставляя (2.14) , (2.11) и (2.10) в (2.8) получим:
 | (2.15) |
Для решения этой системы нужно выразить скорость и ускорение массы m через их составляющие:
 . | (2.16) |
Поскольку в манипуляторе суммарную жесткость удобно экспериментально определять, прикладывая соответствующее усилие к его рабочему органу, и так как в конечном итоге необходимо определить положение массы m , координаты которой выражаются как , то для этого достаточно сложить уравнения в выражении (2.15):
 | (2.17) |
или:
 , | (2.18) |
где С - суммарная жесткость звеньев манипулятора.
Анализ показывает, что величина C является переменной и зависит от плеча приложения l сосредоточенной массы m .
Преобразуя (2.18), получаем уравнение описывающие переходный процесс в системе:
 . | (2.19) |
Уравнение (2.19) легко решается классическим способом при следующих начальных условиях:
  , | (2.20) |
где 
- скорость рабочего органа манипулятора в момент выхода на конечную точку.
Выражение (2.19) представляет собой линейное дифференциальное уравнение второго порядка. Будем искать частное решение уравнения в виде:
 , | (2.21) |
где 
и 
- произвольные постоянные, которые могут быть определены из начальных условий: при t = 0; 
и 
- корни характеристического уравнения:
 . | (2.22) |
Решение уравнения (2.22) будет иметь вид:
 | (2.23) |
Определим произвольные постоянные 
и 
, решая систему уравнений:
 . | (2.24) |
Решение системы (2.24) будет иметь вид:
 , | (2.25) |
если учесть (2.20) то:
 | (2.26) |
подставляя (2.26) в (2.21) и с учетом (2.23) имеем:
 | (2.27) |
где 
- реальная часть; 
- мнимая часть.
Тогда разделяя реальную и мнимую части в (2.27) получим:
 . | (2.28) |