Реферат: Поверхневі напівпровідникові хвилі в напівпровідникових структурах

У випадку обмеженого кристала виникає можливість існування електромагнітних хвиль іншого типу - бежучих по поверхні , що не заглиблюються в кристал і є ніби “прив`язаними” до поверхні. Такіхвилі логічно назвати “поверхневими” на противагу “об`ємним”, що існують у глибині кристала і не відчувають впливу його поверхні. Відсутність ефекту розповсюдження та розпливання, дифракції у напрямку, нормальному до поверхні кристала,автоматично викликає за собою затухання поля вздовж нормалі вглиб кристала. В цьому також проявляється поверхневий характер хвилі .

Однією з найважливіших характеристик хвильового процесу є залежність швидкостірозповсюдження від довжини хвилі ,тобто їх дисперсія.Оскільки , де - кругова частота коливань, що розпосюджуються в даному хвильовому процесі , а - довжина хвильового вектора , дисперсія хвиль еквівалентна взаємозв`язку величин і k. Цей взаємозв`язок називають законом дисперсії для даної хвилі.

Отже, поверхневий поляритон є нормальною поверхневою електромагнітною хвилею в кристалі. Термін “нормальна” означає , що хвиля задовольняє макрорівнянням Максвелла. Однак електромагнітне поле поблизу границі кристала повинне задовольняти також відомим граничним умовам, якізв`язуютькомпонентивекторів поля по обидві сторони від границі. Звідси випливає те, що поле зовні кристала, в середовищі, що граничить з кристалом, також відмінне від нуля. Поверхневий характер хвилі означає відсутність ефектів розповсюдження і в напрямі зовнішньої по відношенню до кристалу нормалі до його поверхні і затухання поля ПП в цьому напрямі.

Таким чином, поле ПП локалізовано по обидві сторони від поверхні кристала і затухає при віддаленні віднеїв довільну сторону. Потік енергії для хвилі ППє тангенціальним до поверхні кристала.

3. Метод порушеного повного відбивання (ППВВ)

Дослідження поверхневих поляритонів в напівпровідниках та діелектриках проводиться за допомогою методів повного внутрішнього відбивання (ППВВ), розсіяння повільних електронів , а також комбінаційного розсіяння світла (КРС). Всі ці методи засновані на різних фізичних явищах та мають рзну точність. Тим не менш, всі вони доповнюють один одного та дозволяють вивчати спектри поверхневих хвиль в широкому інтервалі довжин хвиль.

При розповсюдженні світлової хвилі з оптично більш густого середовища 1 в менш густе 2 () на межі двох середовищ виникає явище повного внутрішнього відбивання , якщо кут падіння , більше критичного . Однак при цьому поле в середовищі 2 не дорівнює нулю , а є затухаючим (неоднорідним) : , (3.1)

де -амплітуда поля на межі розподілу; - ефективна глибина проникнення поля в менш гуте середовище. Без урахування поглинання величина визначається за формулою

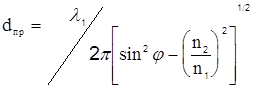,(3.2)

де - довжина хвилі світла в середовищі 1.

З формули (3.2) легко бачити, що зі збільшенням в залежності від глибина проникнення зменшується та має порядок довжини хвилі . Якщо при цьому граничне середовище є поглинаючим , то повного внутрішнього відбивання не відбувається (R<1) та говорять про порушене внутрішнє відбивання світла.

По класичним рівнянням Френеля можна розрахувати величину послаблення коефіцієнта відбивання R, якщо використовувати для середовища 2 уявний показник заломлення . Спектральний розподіл так званого контраста спектра ППВВ=1 R несе інформацію про оптичне поглинання в середовищі 2 , що торкається призми ППВВ=1 , широко використовується для дослідження складу та інших характеристик середовищ ( плівок), осаджених на призму зв`язку.

Метод ППВВ був вперше використаний для дослідження поверхневих плазмонів в металах у 1968 р. Потім було звернено увагу на можливості використання цього метода для вивчення поверхневих фононів. Методом ППВВ експериментально досліджувались спектри ПП в кубічних кристалах. В однорідних кристалах спектри ПП вивчено лиш для декількох орієнтацій поверхні.

В нерадіаційній ділянці спектру моди поверхневих коливань в кристалах характеризуються тим, що вони не взаємодіють безпосередньо з падаючим світлом , бо їх дисперсійні криві лежать в такій області, де неиожливо одночасно виконати закони збереження енергії та імпульса . Тут - частота ПП, - частота світла, - хвильові вектори ПП та світла в площині кристала. Дійсно, комбінуючи ці два вирази, отримаємо , де - діелектрична проникність зовнішнього середовища, а вісь z напрямлена по нормалі до поверхні. З іншого боку , для нерадіацайних мод має місце співвідношення . Виконання останніх двох умов при неможливе.

Наведені вище міркування показують, що закони збереження імпульсу та енергії, з одного боку, та вид дисперсійних кривих , з іншого, не протирічать одне одному лише в тому випадку, коли , тобто , якщо електромагнітна хвиля затухає вздовж вісі z в просторі над досліджуваним кристалом. Така неоднорідна хвиля виникає при повному внутрішньому відбиванні на межі оптично більш густіших та менш густіших середовищ. Ця хвиля розповсюджується вздовж границі розподілу двох середовищ в площині падіння та експоненційно затухає в напрямі оптично менш густого середовища на відстані порядку довжини хвилі. В напрямі розповсюдження вздовж границі розподілу фазова швидкість хвилі, що пройшла, рівна 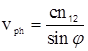, де - кут падіння світла на границю розподілу , а величина відносного оптичного показника заломлення 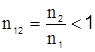. На границі оптично більш густого середовища 1 з вакуумом (середовище 2) 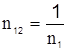, та при зміні кута падіння від критичног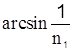о до змінюється від c до , що і лежить в основі методу ППВВ.

В експерименті вимірювався коефіцєнт відбивання електромагнітної хвилі, що падає на поверхню розподілу двох середовищ (призми та зазора), котра є площиною повного внутрішнього відбивання ( рис. 3.1). Наявність поглинаючого середовища (тобто кристала, в якому вивчався спектр поверхневих хвиль) призводить до зменшення інтенсивності відбитого світла. В зазорі між призмою та кристалом розповсюджується електромагнітна хвиля зі зменшеною фазовою швидкістю , де n - показник заломлення призми. При цьому умова повного внутрішнього відбивання порушується , бо виникає поглинання світла , коефіцієнт відбивання стає менше 1. В спектрі спостерігаються мінімуми , положення яких при виконанні деяких умов відповідають частотам поверхневих поляритонів , де визначається проекцією падаючої хвилі на напрям розповсюдження :

, (3.1)

Виміри дозволяють зняти дисперсійні залежності .

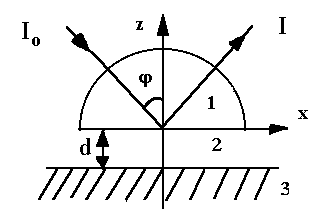
Рис. 3.1 Геометрія досліду по дослідженню поверхневих

коливань методом ППВВ:

1 - призма,

2 - зазор,

3 - досліджуваний кристал.

При цьому падаюча хвиля поляризована в площині падіння (P - поляризація).

Результати досліджень показали, що коли досить точно відомі значення частотно залежної комплексної величини значення поверхневих частот може бути передбачене з досить високою точністю з розрахунку.

Поглинання світла обумовлене наявністю двох механізмів уширення моди поверхневих коливань. Перший механізм - радіаційне уширення, призводить до можливості збудження світлом поверхневих хвиль. Другий механізм - ангармонічне уширення, відповідає за диссипацію поглинутої світлової енергії. Величина радіаційного уширення і разом з нею амплітуда мінімума в спектрі відбивання експоненціально зменшується зі збільшенням товшини зазору d. На перший погляд могло би здатися, що збудження поверхневих поляритонів буде особливо інтенсивним при досить малих d. В дійсності ж при d=0 ці хвилі взагалі не збуджуються .

Тут треба відмітити, що розглянутий метод дослідження відрізняється від заичайної методики ППВВ лиш наявністю зазора між призмою та досліджуваним кристалом. Його наявність необхідна для вивчення нерадіаційних мод. Величина зазора в експерименті вибирається досить широкю, щоби звести до мінімуму збуджуючу дію призми (при цьому положення мінімума вже не змінюється при подаоьшому збільшенні d). Оптимальне значення d підбирається експериментально , воно різне для різних j , тобто для різних , Фіксуючи положення мінімумів в спектрах ППВВ для різних можна досліджувати дисперсійні залежності .В практиці роботи з ІЧ спектрометрами виявилось зручно сканувати по частоті при фіксованому куті падіння.

Розрахунки спектрів ППВВ для поверхневих мод було проведено в ряді робіт. При цих розрахунках діелектрична проникність кристала вважалася уявною: