Реферат: Правильные многогранники
Сумма плоских
углов при вершине
Правильный
треугольник
Правильный
треугольник
Правильный
треугольник
Квадрат
Правильный
гексаэдр (куб)
Правильный
пятиугольник
ёПравильный
додекаэдр
У каждого из правильных многогранников, помимо уже указанных, нас чаще всего будут интересовать:
1. Величина его двугранного угла при ребре (при длине ребра a ).
2. Площадь его полной поверхности (при длине ребра a ).
3. Его объем (при длине ребра a ).
4. Радиус описанной около него сферы (при длине ребра a ).
5. Радиус вписанной в него сферы (при длине ребра a ).
6. Радиус сферы, касающихся всех его ребер (при длине ребра a ).
Наиболее просто решается вопрос о вычислении площади полной поверхности правильного многогранника; она равна Г
, где Г – количество граней правильного многогранника, а 
- площадь одной грани.
Напомним, sin
= 
, что дает нам возможность записать в радикалах: ctg
=
. Учитывая это составляем таблицы:
а) для площади грани правильного многогранника
| Вид грани | Длина стороны | Длина апофемы грани | Площадь грани |
| Правильный треугольник | a | 0,5 |  |
| Квадрат | a | 0,5a |  |
| Правильный пятиугольник | a |  |  |
б) для площади полной поверхности правильного многогранника
| Вид многогранника | Вид граней | Количество граней | Площадь полной поверхности |
| Правильный тетраэдр | Правильный треугольник | 4 |  |
| Правильный октаэдр | Правильный треугольник | 8 |   |
| Правильный икосаэдр | Правильный треугольник | 20 |  |
| Правильный гексаэдр (куб) | Квадрат | 6 | 6a |
| Правильный додекаэдр | Правильный пятиугольник | 12 |  |
Теперь перейдем к вычислению величины двугранного угла 
правильного многогранника при его ребре. Для правильного тетраэдра и куба вы легко найдете величину этого угла.
В правильном додекаэдре все плоские углы его граней равны , поэтому, применив теорему косинусов для трехгранных углов к любому трехгранному углу данного додекаэдра при его вершине, получим: cos
, откуда
.
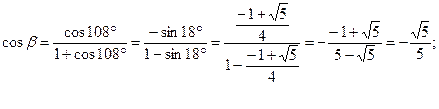