Реферат: Правильные многогранники

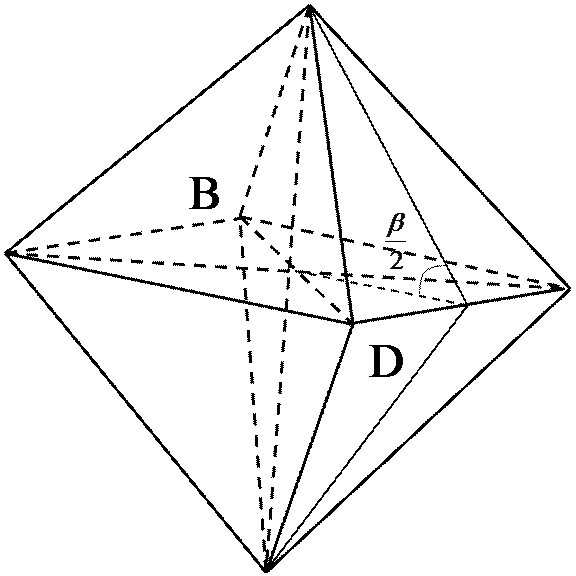
F

Для нахождения величины двугранного угла при ребре правильного икосаэдра можно рассмотреть трехгранный угол ABCD при вершине А: его плоские углы ВАС и CAD равный , а третий плоский угол BAD, против которого лежит двугранный угол B(AC)D = , равен (BCDMF– правильный пятиугольник). По теореме косинусов для трехгранного угла ABCDимеем: . Учитывая, что , получаем , откуда . Таким образом, двугранный угол при ребре икосаэдра равен .

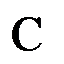
Итак, получаем следующую таблицу величин двугранных углов при ребрах правильных многогранников.

Вид многогранника	Величина двугранного угла при ребре
Правильный тетраэдр
Правильный октаэдр
Правильный гексаэдр (куб)
Правильный додекаэдр
Правильный икосаэдр

Прежде чем находить объем того или иного правильного многогранника, сначала проведем рассуждения о том, как можно найти объем правильных многогранников в общем виде.

Попытайтесь сначала доказать, что если центр каждой грани любого правильного многогранника провести прямую, перпендикулярную плоскости этой грани, то все проведенные прямые пересекутся в некоторой одной точке О , удаленной от всех граней данного многогранника на одно и тоже расстояние, которое обозначим r. Точка О окажется центром сферы, вписанной в данный многогранник, а r – ее радиусом. Соединив полученную точку О со всеми вершинами данного многогранника, мы разобьем его на Г равных между собой пирамид (Г—число граней правильного многогранника): основаниями образованных пирамид равны r . Тогда объем данного многогранника равен сумме объемов всех этих пирамид. Так как многогранник правильный, то его объем V можно найти по формуле:

(1)

Остается найти длину радиуса r . Для этого, соединив точку О с серединой К ребра многогранника, попробуйте убедиться, что наклонная КО к грани многогранника, содержащей ребро, составляет с плоскостью этой грани угол, равный половине величины двугранного угла при этом ребре многогранника; проекция же наклонной КО на плоскость этой грани принадлежит ее апофеме и равна радиусу вписанной в нее окружности. Тогда

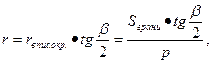
(2)
где p —полупериметр грани. Тогда из (1) и (2) получаем общую для всех правильных многогранников формулу вычисления их объемов:

.

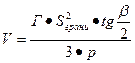Эта формула совершенно не нужна для нахождения объемов куба, правильных тетраэдра и октаэдра, но позволяет довольно легко находить объемы правильных икосаэдра и додекаэдра.

Вид многогранника	Объем многогранника
Правильный тетраэдр
Правильный октаэдр
Куб
Правильный икосаэдр
Правильный додекаэдр

Министерство образования РФ г. Янаул

по геометрии на тему «Правильные многогранники».

Выполнил: Хабибьянов Д.Р.

Проверила: Нургаянова Т.С.

2004 год.