Реферат: Предельные теоремы. Характеристические функции

Теорема Чебышева. При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины, имеющих конечную дисперсию, сходится по вероятности к ее математическому ожиданию.

Определение. Случайные величины сходятся по вероятности к величине а, если для , начиная с которого выполняется неравенство или, по другому, если для любого малого

Итак, нужно доказать, что для любого малого

Доказательство. Введем случайную величину

Найдем числовые характеристики случайной величины Y, пользуясь их свойствами:

Теперь применим неравенство Чебышева к случайной величине Y:

Так как по условию D_x ограничена, то

Прежде чем сформулировать центральную предельную теорему введем характеристические функции.

2. Характеристические функции

Характеристические функции являются одним из способов описания случайных величин, удобным при решении многих задач теории вероятностей.

Пусть имеется вещественная случайная величина Х. Введем комплексную случайную величину W по следующему закону:

где .

Характеристической функцией g(t) случайной величины Х называется математическое ожидание случайной величины W, т.е.

Зная закон распределения случайной величины Х, всегда можно найти ее характеристическую функцию g(t).

Для дискретной случайной величины Х с законом распределения

Таблица 1

Х	х1	х2	...	хn
Р	p1	p2	...	pn

характеристическая функция

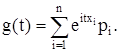
Для непрерывной случайной величины с плотностью распределения вероятностей f(x) характеристическая функция

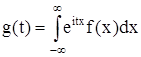
является преобразованием Фурье плотности распределения f(x). С помощью обратного преобразования Фурье можно найти плотность распределения