Реферат: Предельные теоремы. Характеристические функции

Для того, чтобы эти формулы можно было применять требуется, чтобы

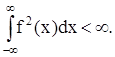
В качестве примера найдем характеристическую функцию нормированной гауссовсокой случайной величины. Случайная величина Х называется нормированной, если ее числовые характеристики m_x =0 и D_x =1. Плотность распределения вероятности нормированной гауссовской случайной величины имеет вид:

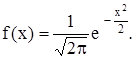
По определению имеем

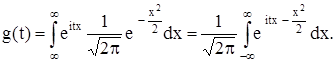(2)

После преобразования

и замены в интеграле

z = x – jt

соотношение (2) принимает вид

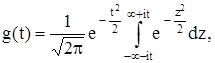
но так как

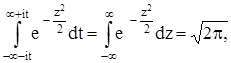
то

Таким образом, характеристическая функция с точностью до постоянного множителя совпадает с плотностью распределения.

2.1 Свойства характеристической функции

1. Характеристическая функция g(t) вещественна тогда и только тогда, когда f(x) – четная функция. Причем g(t) также четна. Это следует из свойств преобразования Фурье.

2. Если случайные величины Х и Y связаны соотношением

Y = aX,

где а – постоянный множитель, то

g_y (t) = g_x (at).

Доказательство.

3. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций.

Доказательство. Пусть Х₁ , Х₂ , ... , Х_n - независимые случайные величины с характеристическими функциями g_{x 1} (t), g_{x 2} (t), ... , g_xn (t).

Найдем характеристическую функцию