Реферат: Приложения производной

Ясно, что производная функции y =f (x) есть также функция от x :

Если функция f ' (x) дифференцируема, то её производная обозначается символом y'' =f '' (x) и называется второй производной функции f(x) или производной функции f(x) второго порядка. Пользуясь обозначениемможем написать

Очень удобно пользоваться также обозначением, указывающим, что функция y=f(x) была продифференцирована по x два раза.
Производная второй производной, т.е. функции y''=f '' (x) , называется третьей производной функции y=f(x) или производной функции f(x) третьего порядка и обозначается символами.

Вообще n -я производная или производная n -го порядка функции y=f(x) обозначается символами

Дифференцируя производную первого порядка, можно получить производную второго порядка, а, дифференцируя полученную функцию, получаем производную третьего порядка и т.д. Тогда возникает вопрос: сколько производных высших порядков можно получить в случае произвольной функции.

Например:

1) ; ; ; ...;

; .

Разные функции ведут себя по-разному при многократном дифференцировании. Одни имеют конечное количество производных высших порядков, другие – переходят сами в себя, а третьи, хотя и дифференцируемы бесконечное количество раз, но порождают новые функции, отличные от исходной.

Однако все сформулированные теоремы о производных первых порядков выполняются для производных высших порядков.

6. Изучение функции с помощью производной

6.1.Возрастание и убывание функции. Экстремум функции.

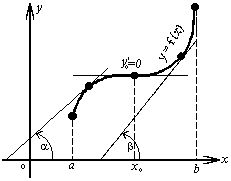
Определение 1. Функция f(x) называется возрастающей в интервале (a,b) , если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если f(x₂ ) > f(x₁ ) при x₂ > x₁ .

Рис.1 (а)

Рис.1 (б)

Из этого определения следует, что у возрастающей в интервале (a,b) функции f(x) в любой точке этого интервала приращения Dx и Dy имеют одинаковые знаки .
График возрастающей функции показан на рисунке1(а).
Если из неравенства x₂ > x₁ вытекает нестрогое неравенство f (x₂ ) ³f (x₁ ) , то функция f (x) называется неубывающей в интервале (a, b ) . Пример такой функции показан на рисунке 2(а). На интервале [ x₀ , x₁ ] она сохраняет постоянное значение C
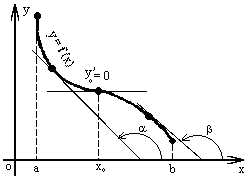
Определение 2. Функция f (x) называется убывающей в интервале ( a, b ) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если f(x₂ ) < f(x₁ ) при x₂ > x₁ .

Из этого определения следует, что у убывающей в интервале ( a, b ) функции f (x) в любой точке этого интервала приращения Dx и Dy имеют разные знаки . График убывающей функции показан на рисунке 1(б).

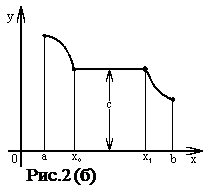
Если из неравенства x₂ > x₁ вытекает нестрогое неравенство f(x₂ ) £ f(x₁ ) , то функция f (x) называется невозрастающей в интервале ( a, b ) . Пример такой функции показан на рисунке 2(б). На интервале [ x₀ , x₁ ] она сохраняет постоянное значение C .

Теорема 1. Дифференцируемая и возрастающая в интервале ( a, b ) функция f (x) имеет во всех точках этого интервала неотрицательную производную .
Теорема 2. Дифференцируемая и убывающая в интервале ( a, b ) функция f (x) имеет во всех точках этого интервала неположительную производную .

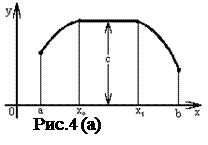Пусть данная непрерывная функция убывает при возрастании x от x₀ до x₁ , затем при возрастании x от x₁ до x₂ - возрастает, при дальнейшем возрастании x от x₂ до x₃ она вновь убывает и так далее. Назовем такую функцию колеблющейся .
График колеблющейся функции показан на рисунке 3. Точки A, C, в которых функция переходит от возрастания к убыванию, так же, как и точки B, D, в которых функция переходит от убывания к возрастанию, называются точками поворота или критическими точками кривой y = f (x) , а их абциссы - критическими значениями аргумента x
В той точке, где функция переходит от возрастания к убыванию, ордината больше соседних с ней по ту и другую сторону ординат. Так, ордината точки A больше ординат, соседних с ней справа и слева и достаточно к ней близких, т.е. значение функции в точке A , абсцисса которой равна x₀ , больше значений функции в точках, абсциссы которых достаточно близки к x₀ : f (x₀ ) > f (x₀ + ∆x) .

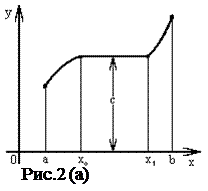
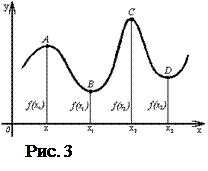
На рисунке 4(a) изображена функция f (x) , непрерывная в интервале ( a, b ) . В интервале ( a, x₀ ] она возрастает, на интервале [ x₀ , x₁ ] - сохраняет постоянное значение: f (x₀ ) = f (x₁ ) = C , в интервале [ x₁ , b ) - убывает. Во всех точках, достаточно близких к x₀ (или x₁ ), значения функции f (x) удовлетворяют нестрогому неравенству f (x₀ ) ³f (x) .

Значение f (x₀ ) функции f (x) , при котором выполняется вышеуказанное неравенство, называется максимальным значением функции f (x) или просто максимумом.
Определение 3. Максимумом функции f (x) называется такое значение f (x₀ ) этой функции, которое не меньше всех значений функции f (x) в точках x , достаточно близких к точке x₀ , т.е. в точках x ,

принадлежащих некоторой достаточно малой окрестности точки x₀ .
Так, на рисунке 3 показаны два максимума: f (x₀ ) и f (x₂ ) .
В той точке, где функция переходит от убывания к возрастанию, ордината меньше ординат в достаточно близких к ней точках, расположенных справа и слева от нее. Так ордината точки B меньше ординат в точках соседних и достаточно близких к точке x₁ справа и слева. Значение функции в точке, абсцисса которой равна x₁ , меньше значений функции в точках, абсциссы которых достаточно мало отличаются от x₁ : f (x₁ ) < f (x₁ + Dx) .

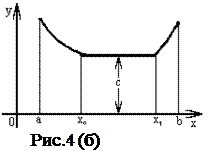
На рисунке 4(б) изображена функция f (x) , непрерывная в интервале ( a, b ) . В интервале ( a, x₀ ] она убывает, на интервале [ x₀ , x₁ ] - сохраняет постоянное значение: f (x₀ ) = f (x₁ ) = C , в интервале [ x₁ , b ) - возрастает. Во всех точках, достаточно близких к x₀ (или x₁ ), значения функции f (x) удовлетворяют нестрогому неравенству f (x₀ ) £f (x) .

Значение f (x₀ ) функции f (x) , при котором выполняется вышеуказанное неравенство, называется минимальным значением функции f (x) или просто минимумом.
Определение 4. Минимумом функции f (x) называется такое значение f (x₀ ) этой функции, которое не больше всех значений функции f (x) в точках x , достаточно близких к точке x₀ , т.е. в точках x , принадлежащих некоторой

достаточно малой окрестности точки x₀ .
Так, на рисунке 3 показаны два минимума: f (x₁ ) и f (x₃ ) .
По определению наибольшим значением функции f (x) на интервале [ a, b ] является такое значение f (x₀ ) , для которого для всех точек интервала [ a, b ] выполняется неравенство f (x₀ ) ³f (x) , а наименьшим значением функции f (x) на интервале [ a, b ] является такое значение f (x₀ ) , для которого для всех точек интервала [ a, b ] выполняется неравенство f (x₀ ) £f (x) .
Из этих определений следует, что функция может достигать своего наибольшего или наименьшего значения как внутри интервала [ a, b ] , так и на его концах a и b . Здесь же максимум и минимум функции f (x) были определены соответственно как наибольшее и наименьшее значения в некоторой окрестности точки x₀ .
Если в точке x₀ функция f (x) достигает максимума или минимума, то говорят, что функция f (x) в точке x₀ достигает экстремума (или экстремального значения) .
Функция f (x) может иметь несколько экстремумов внутри интервала [ a, b ] , причем может оказаться, что какой-нибудь минимум будет больше какого-нибудь максимума. Таким образом, наибольшее значение функции f (x) на интервале [ a, b ] - это наибольший из экстремумов функции внутри этого интервала и наибольшее из значений функции на концах интервала .
Аналогично наименьшее значение функции f (x) на интервале [ a, b ] - это наименьший из экстремумов функции внутри этого интервала и наименьшее из значений функции на концах интервала .

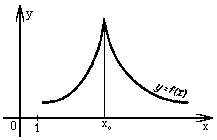
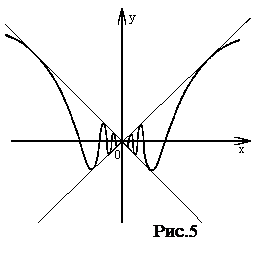
Например функция, изображенная на рисунке 3, достигает наибольшего значения f (x) в точке x₂ , наименьшего - в точке x₁ интервала [ x₀ , x₃ ] . На рисунке 5 изображена функция, имеющая бесконечное число минимумов и максимумов.

Теорема 3 (необходимый признак экстремума). Если функция f (x) имеет в точке x₀ экстремум, то ее производная в данной точке или равна нулю или не существует .
Но функция f (x) может иметь экстремумы и в тех точках x₀ , в которых ее производная не существует. Например функция y = | x | в точке x₀ = 0 не дифференцируема, но достигает минимума. Точки такого типа называют угловыми . В них кривая не имеет определенной касательной.

Рис. 6

На рисунке 6 изображена функция f (x) , не имеющая в точке x₀ производной [f' (x₀ ) = ¥] и достигающая в этой точке максимума. При x ®x₀ и x < x₀ f' (x) ® +¥, при x ®x₀ и x > x₀ f' (x) ® -¥. Значит касательная кривой y = f (x) при x = x₀ перпендикулярна к оси Ox . Такие точки называются точками возврата кривой y=f(x) .
Таким образом, необходимым признаком существования в точке x₀ экстремума функции f (x) является выполнение следующего условия: в точке x₀ производная f' (x) или равна нулю, или не существует.
Этот признак не является достаточным условием существования экстремума функции f (x) в точке x₀ : можно привести много примеров функций, удовлетворяющих этому условию при x = x₀ , но, однако, не достигающих экстремума при x = x₀ .
Например, производная функции y = x³ при x₀ = 0 равна нулю, однако эта функция при x₀ = 0 не достигает экстремального значения.

6.2.Достаточные условия убывания и возрастания функции. Достаточные условия экстремума функции.

Теорема 4. Если функция f(x) имеет в каждой точке интервала (a, b) неотрицательную производную, то она является неубывающей функцией в этом интервале.
Теорема 5. Если функция f(x) в каждой точке интервала (a, b) имеет неположительную производную, то она является невозрастающей функцией в этом интервале.