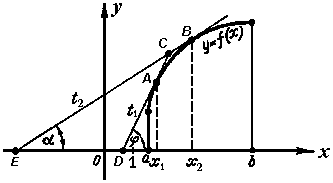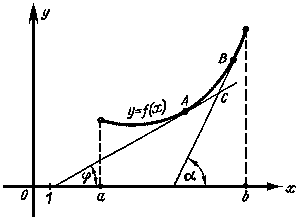Реферат: Приложения производной
6.3 .Правило нахождения экстремума
1° . Чтобы найти экстремум функции, надо:
1) найти производную данной функции;
2) приравнять производную нулю и решить полученное уравнение; из полученных корней отобрать действительные и расположить их (для удобства) по их величине от меньшего к большему; в том случае, когда все корни оказываются мнимыми, данная функция не имеет экстремума;
3) определить знак производной в каждом из промежутков, отграниченных стационарными точками ( стационарными точками называют точки в которых производная равна 0);
4) если производная положительна в промежутке, лежащем слева от данной стационарной точки, и отрицательна в промежутке, лежащем справа от нес, то данная точка есть точка максимума функции, если же производная отрицательна слева и положительна справа от данной стационарной точки, то данная точка есть точка минимума функции; если производная имеет один и тот же знак как слева, так и справа от стационарной тонки, то в этой точке нет ни максимума, ни минимума, функции;
5) заменить в данном выражении функции аргумент значением, которое дает максимум или минимум функции; получим значение соответственно максимума или минимума функции.
Если функция имеет точки разрыва, то эти точки должны быть включены в число стационарных точек, разбивающих Ох на промежутки, в которых определяется знак производной.
Будем говорить, что кривая y = f(x) в точке x0 обращена выпуклостью вверх, если существует такая окрестность точки x0 , что часть кривой, соответствующая этой окрестности, лежит под касательной к этой кривой, проведенной в точке A с абсциссой x0 . (см. Рисунок 1а ).
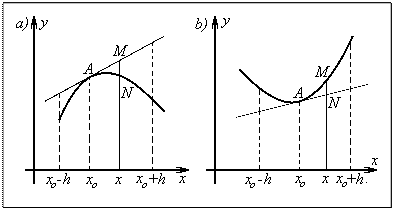 Рисунок 1 Рисунок 1 |
Будем говорить, что кривая y = f(x) в точке x0 обращена выпуклостью вниз, если существует такая окрестность точки x0 , что часть кривой, соответствующая этой окрестности, лежит над касательной к этой кривой, проведенной в точке A с абсциссой x0 . (см. Рисунок 1б ).
Из определения выпуклости вверх (вниз) кривой y = f(x) в точке x0 следует, что для любой точки x из интервала (x0 - h, x0 + h) , не совпадающей с точкой x0 , имеет место неравенство f(x) - y < 0 ( f(x) - y > 0) где f(x) - ордината точки M кривой y = f(x) , y - ордината точки N касательной y - y0 = f '(x0 )(x - x0 ) к данной кривой в точке A . (смотри рисунок 1, а, б ).
Ясно, что и наоборот, если для любой точки x интервала (x0 - h, x0 + h) , не совпадающей с x0 , выполняется неравенство f(x) - y < 0 (f(x) - y > 0) ,
то кривая y = f(x) в точке x0 обращена выпуклостью вверх (вниз).
Будем называть кривую y = f(x) выпуклой вверх (вниз) в интервале (a, b) , если она выпукла вверх (вниз) в каждой точке этого интервала.
Если кривая y = f(x) обращена выпуклостью вверх в интервале (a, b) , то с увеличением аргумента x угловой коэффициент касательной к этой кривой в точке с абсциссой x будет уменьшаться.
|
Рисунок 2. |
В самом деле, пусть абсцисса x1 точки A меньше абсциссы x2 точки B (рис. 2). Проведем касательные t1 и t2 соответствено в точках A и B к кривой y = f(x) . Пусть a и j - углы наклона касательных t1 и t2 . Тогда из рис. 2 видим, что j - внешний угол треугольника ECD , а поэтому он больше угла a. Следовательно tg j > tg a или f '(x1 ) > f '(x2 ) .
Таким образом мы показали, что если в интервале (a, b) кривая y = f(x) обращена выпуклостью вверх, то с увеличением аргумента x функция y = f '(x) убывает. Поэтому вторая производная f ''(x) функции f(x) , как производная убывающей фунции f '(x) , будет отрицательна или равна нулю в интервале (a, b) : f ''(x) £0 .
|
Рисунок 3. |
Если кривая y = f(x) обращена выпуклостью вниз, то из рис.2 непосредственно видно, что tg a > tg j т.е. f '(x2 ) > f '(x1 ) , а поэтому в интервале (a, b) производная f '(x) возрастает. Тогда вторая производная f ''(x) функции f (x) , как производная возрастающей в интервале (a, b) функции f '(x) , будет положительна или равна нулю: f ''(x) ³0 .
Докажем, что и наоборот, если f ''(x) £0 в некотором интервале (a, b) , то в этом интервале кривая y = f (x) обращена выпуклостью вверх; если f ''(x) ³0 в интервале (a, b) , то в этом интервале кривая обращена выпуклостью вниз.
Запишем уравнение касательной y - y0 = f '(x0 )(x - x0 ) к кривой y = f (x) в точке x0 , где a < x0 b , в виде y = y0 + f '(x0 )(x - x0 ). Очевидно, y0 = f(x0 ) , а потому последнее уравнение можно записать в виде y = f(x0 ) + f '(x0 )(x - x0 ) . (1)
Но, согласно формуле Тейлора, при n = 2 имеем:
![]() (2)
(2)
Фиксируя x в интервале (a, b) и вычитая почленно из уравнения (2) уравнение (1), получим:![]() (3)
(3)
Если f '' [x0 + Q(x - x0 ) ]£0 , где 0 < Q < 1 , то имеем f(x) - y £ 0
откуда следует, что кривая y = f(x) в точке x обращена выпуклостью вверх.
Если f '' [x0 + Q(x - x0 ) ]³0 , то имеем f(x) - y ³ 0 откуда следует, что кривая y = f(x) в точке x обращена выпуклостью вниз.
Так как была зафиксирована произвольная точка x интервала (a, b) , то высказанное выше утверждение доказано.
|
Рисунок 4. |
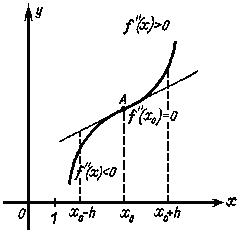
Точка кривой, в которой кривая меняет направление изгиба, т.е. переходит от выпуклости вверх к выпуклости вниз или наоборот, называется точкой перегиба кривой (рис.4). (В этом определении предполагается, что в точке перехода кривой от выпуклости вверх к выпуклости вниз (или наоборот) имеется единственная касательная).
Теорема 8. Пусть функция f(x) имеет непрерывную вторую производную f ''(x) и пусть A [x0 ; f(x0 ) ] - точка перегиба кривой y = f(x) . Тогда f ''(x0 ) = 0 или не существует.
Доказательство. Рассмотрим для определенности случай, когда кривая y = f(x) в точке перегиба A [x0 ; f(x0 ) ] переходит от выпуклости вверх в выпуклости вниз (рис.4). Тогда при достаточно малом h в интервале (x0 - h, x0 ) вторая производная f ''(x) будет меньше нуля, а в инетрвале (x0 , x0 +h) - больше нуля.
Но f ''(x) - функция непрерывная, а потому, переходя от отрицательных значений к положительным, она при x = x0 обращается в нуль: f ''(x0 ) = 0 .
|
Рисунок 5. |
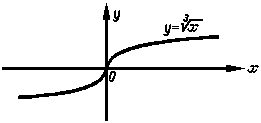
На рис.5 изображен график функции ![]() . Хотя при x0 = 0 имеется касательная и точка перегиба, все же вторая производная f ''(x) не равна нулю, она даже не существует в этой точке. В самом деле, имеем
. Хотя при x0 = 0 имеется касательная и точка перегиба, все же вторая производная f ''(x) не равна нулю, она даже не существует в этой точке. В самом деле, имеем ![]()
Итак, f ''(0) не существует. Но тем не менее точка O(0; 0) является точкой перегиба, так как при x < 0 f ''(x) > 0 и кривая выпукла вниз, а при x > 0 f ''(x) < 0 и кривая выпукла вверх.
Таким образом в случае непрерывности второй производной f ''(x) обращение в нуль или несуществование ее в какой-нибудь точки кривой y = f(x) является необходимым условием существования точки перегиба. Однако это условие не является достаточным.
Теорема 9. Если вторая производная f ''(x) непрерывна и меняет знак при x = x0 , то точка A [x0 ; f(x0 ) ] является точкой перегиба кривой y = f(x) при условии, конечно, что в точке A существует касательная .
Доказательство. Пусть например f ''(x) < 0 при x0 - h < x < x0 и f ''(x) > 0 при x0 < x < x0 + h . Тогда в интервале (x0 - h; x0 ) кривая y = f(x) обращена выпуклостью вверх, а в интервале (x0 ; x0 + h) - выпклостью вниз (смотри рис.4), т.е. точка A [x0 ; f(x0 ) ] есть точка перегиба кривой, что и требовалось доказать.
6.5.Общая схема исследования функции и построение ее графика.
1. Находим область определения функции f(x)
2. Находим точки пересечения кривой y = f(x) с осями координат и наносим их на чертеж.
3. Определяем, симметрична ли кривая y = f(x) относительно осей координат и начала координат.
4. Исследуем функцию y = f(x) на непрерывность. Если функция имеет в точке x0 разрыв, то отмечаем ее на чертеже.
5. Находим асимптоты кривой, если они имеются.
6. Находим максимум и минимум функции и отмечаем на чертеже точки кривой с максимальной и минимальной ординатами.
7. Исследуем кривую y = f(x) на выпуклость вверх или вниз, находим точки перегиба кривой и отмечаем их на чертеже.
8. Вычерчиваем кривую y = f(x) .
6.6. Касательная и нормаль к плоской кривой.
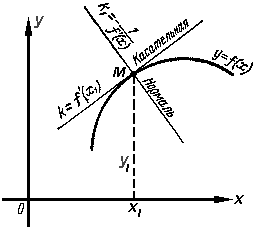 Пусть даны кривая y = f(x) и точка M (x1 ; y1 ) на ней. Требуется составить уравнения касательной и нормали (смотри р
Пусть даны кривая y = f(x) и точка M (x1 ; y1 ) на ней. Требуется составить уравнения касательной и нормали (смотри р