Реферат: Применение геометрического подхода в мембранной теории возбуждения
Совсем другими емкостными свойствами обладает цилиндрическое волокно. Формулы для нарастания и спада тока становятся довольно сложными, и мы их приводить здесь не будем. Суть дела состоит в том, что при тех же самых свойствах мембраны, что и у сферической клетки, потенциал в кабеле и нарастает, и спадает гораздо быстрее.
Ну и что? Первые примеры влияния геометрии на функции
Какое значение имеют эти системные свойства для работы нейронов и волокон? В чем проявляется их различие? Приведем несколько примеров, показывающих важное значение системных параметров для работы нейронов.
Пример первый. Пусть у нас есть две сферические клетки — большая и маленькая, и на обеих клетках имеются одинаковые синапсы. Спрашивается, какое влияние окажут эти синапсы на разные клетки?
Формула для сдвига потенциала, вызываемого в клетке воздействием синапса — постсинаптического потенциала:
![]() . Там же мы указывали, что Ис
. Там же мы указывали, что Ис
очень велико и равно примерно 1012 Ом. Входное сопротивление нейронов гораздо меньше: у нейрона диаметром 1 мм оно порядка 108 Ом и даже у маленького нейрона диаметром всего 10 мкм оно составляет только 109 Ом. Следовательно, в знаменателе вышеприведенной формулы /?вх мало по сравнению с Ис и им можно пренебречь. Мы получаем упрощенную формулу
![]()
Как видно из этой формулы, постсинаптический потенциал, создаваемый одинаковыми синапсами в разных клетках, будет прямо пропорционален их /?вх , а /?вх сферической клетки, в свою очередь, обратно пропорционально квадрату ее диаметра. Так что при одинаковом воздействии постсинаптический потенциал в клетке диаметром 10 мкм будет в 100 раз больше, чем в клетке диаметром в 100 мкм. Об этой разной восприимчивости к синаптическим воздействиям клеток разного диаметра известный советский ученый М.М. Бонгард сказал: «Это понятно. Спичкой можно зажечь тонкую хворостинку, но нельзя зажечь бревно».
Пример второй. Когда мы разбирали механизм действия тормозных синапсов, то говорили, что они открывают ионные каналы для калия или хлора, что приводит к гиперполяризации клетки, удалению ее потенциала от порогового значения. Теперь мы можем указать вторую причину их тормозного действия. Открывая ионные каналы, тормозные синапсы снижают сопротивление мембраны, а тем самым и Явх нейронов. Из формулы видно, что эффективность действия возбуждающих синапсов тем меньше, чем меньше Я вх, поэтому тормозные синапсы, снижая Явх , снижают эффективность воздействия возбуждающих синапсов.
Но ДВ х сферической клетки и цилиндрического волокна, как видно из формул и, по-разному зависят от сопротивления мембраны. Если тормозные синапсы вдвое снизят сопротивление мембраны сферической клетки, то и Я вх, а значит, и эффективность возбуждающих синапсов тоже снизятся вдвое. Когда же тормозные синапсы действуют на цилиндрический кабель, например на длинный дендрит, результат будет иным: если сопротивление мембраны тоже снизится вдвое, то Я вх снизится только в У 2, т е. примерно в 1,4 раза, а значит, и эффективность торможения будет меньше, чем в случае сферической клетки. Отсюда понятно, почему в организмах тормозные синапсы чаще встречаются на телах нейронов.
Пример третий. Мы видели, что один синапс создает на клетке, даже на очень маленькой, сдвиги потенциала, меньшие порога возбуждения в сотни и даже в тысячи раз. Отсюда следует, что клетка может возбудиться только в результате действия на нее не одного, а многих синапсов.
Когда на клетку примерно одновременно действует много синапсов, находящихся на разных участках ее мембраны, и их действие суммируется, этот процесс называют пространственной суммацией. Однако, как правило, разные синапсы срабатывают неодновременно: один уже кончил действовать, когда другой только начинает. В этом случае процесс называют пространственно-временной суммацией. Чисто временная суммация возникает при действии одного и того же синапса, если к моменту его последующего срабатывания сдвиг потенциала, созданный предыдущим срабатыванием еще не исчез.
Для временной и пространственно-временной суммации очень важно, насколько долго сохраняется «след» от синаптического воздействия, а это зависит от емкостных свойств нейрона. Если возникший потенциал спадает достаточно медленно, то действие второго синапса, включившегося позднее, может суммироваться с остаточным потенциалом от первого. В противном случае суммируется только действие тех синапсов, которые сработали практически одновременно.
Из рис. 43,в ясно, что потенциал в кабеле спадает гораздо быстрее, чем в сферической клетке. Но у беспозвоночных животных синапсы находятся не на телах нервных клеток, а на их отростках, т. е. именно на волокнах, обладающих свойствами кабеля. Отсюда следует, что при одних и тех же свойствах мембраны синаптические потенциалы у беспозвоночных будут суммироваться в меньшей мере, чем на тех нейронах позвоночных, где синапсы находятся на телах клеток. Если же синапсы у позвоночных расположены на длинных дендритах, то суммация будет идти так же, как у беспозвоночных.
Мы рассмотрели две простейшие структуры: сферическую клетку и цилиндрическое волокно. Дальше мы рассмотрим несколько более сложных примеров влияния формы клеток и топологии ткани на их электрические свойства и функции.
Нервное волокно расширяется, сужается, ветвится и кончается
В 1964 г. в Ереване проходил очередной Всесоюзный физиологический съезд. Один из авторов этой книги докладывал на съезде первые результаты и программу исследований, связанных с геометрическим подходом. Среди слушателей был Б.И. Ходоров, сотрудник института хирургии им. А.В. Вишневского, в дальнейшем много сделавший для развития и пропаганды такого подхода. Но тогда он сильно усомнился в правильности выводов, сделанных в докладе о распространении импульсов по неоднородным нервным волокнам, и решил проверить их самостоятельно. Многие выводы этого доклада были сделаны на основании только качественного рассмотрения, так сказать, «на пальцах». Б.И. Ходорсн решил проверить их количественно. Так появилась первая машинная модель проведения импульсов по неоднородным нервным волокнам. Что же удивило Ходорова?
Представим себе, что нервное волокно в некоторой точке резко расширяется. Что произойдет с импульсом, идущим из тонкого участка в толстый? Когда импульс идет по тонкой части волокна, ток, создаваемый возбужденным участком, заряжает мембрану, лежащую рядом с возбужденной областью, и идет по аксоплазме в более удаленные участки. По мере приближения возбужденной области к месту расширения все большая доля тока начинает перетекать в широкую часть волокна — ведь там меньше сопротивление — и меньшая доля тока идет через мембрану невозбужденной области узкого участка волокна. Из-за этого емкость мембраны узкого участка заряжается медленнее, потенциал нарастает медленнее, и импульс замедляет свое движение. Кроме того, снижается и амплитуда импульса, так как при медленном нарастании потенциала успевает инактивироваться часть натриевых каналов.
Пусть теперь импульс подошел вплотную к месту расширения. Условия проведения еще более ухудшаются: ток генерируется мембраной узкой части, а возбудить должен большую по площади мембрану толстой части. Ток, идущий через мембрану широкой части, растекается по большой площади и медленно заряжает ее емкость. В результате потенциал в широкой части волокна будет нарастать очень медленно.
На основании таких соображений авторы доклада и сделали предсказание, что перед расширением импульс должен замедляться и снижать амплитуду, а при некотором критическом расширении вообще не сможет пройти через эту область. Вот эти предсказания и были проверены Б. И. Ходоровым и его сотрудниками с помощью расчетов на вычислительной машине.
Расчеты полностью подтвердили все предсказания. Оказалось, что при расширении волокна в 6 раз ПД не может пройти через это расширение. Шестикратное расширение является критическим, если мембрана волокна точно такая, как у гигантского аксона кальмара; если же эта мембрана более «низкого качества», то блокирование возникает при меньших расширениях.
В дальнейшем задачей о круто или постепенно расширяющихся и сужающихся волокнах занимались многие теоретики и экспериментаторы. Так, сотрудникам Института электрохимии АН СССР В.С. Маркину и Ю.А. Чизмаджеву удалось решить задачу о распространении ПД в волокне с расширением без вычислительной машины, с помощью несколько упрощенной математической модели. Они получили очень неожиданный результат. Оказалось, что если окружить волокно плохо проводящей средой, то ПД может пройти через большее расширение, т. е. если ухудшить условия распространения импульса, то преодоление препятствия облегчается! В чем же тут дело? Грубо говоря, дело в том, Что при увеличении внешнего сопротивления убывает константа длины волокна, и ток не растекается далеко в широкую часть волокна, что облегчает преодоление препятствия.
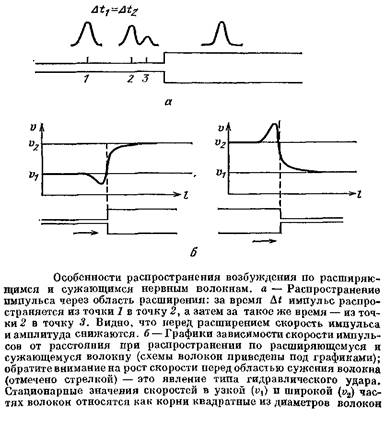
А что будет, если волокно не расширяется, а, напротив, сужается? Повторив рассуждения о расширяющемся во* локне, так сказать, «со знаком минус», легко сообразить, что по мере приближения ПД к месту сужения его скорость должна нарастать, а амплитуда увеличиваться. Это явление оказалось очень важным — ведь к нервным волокнам вполне применима поговорка: «Сколько веревочке ни виться...». Всякий аксон, в конце концов, оканчивается, причем тонкими терминалями, получается как бы «сужение до нуля». Значит, при подходе к терминали импульс все более разгоняется, его амплитуда растет. Возникает явление, похожее на гидравлический удар, когда текущая по трубе жидкость натыкается на препятствие. Возрастание амплитуды потенциала в конце терминали очень важно для работы химических синапсов, так как улучшает условия выделения медиаторов.
Рассмотрим теперь явления в области ветвления нервного волокна.
У позвоночных животных ситуация в области ветвления аксона, как правило, не отличается от случаев расширения и сужения волокна, так как импульс у них возникает в теле клетки и всегда идет от тела по аксону. Если импульс подходит к точке ветвления по толстому стволу, который делится на две тонкие веточки, то ПД перед точкой ветвления ускоряется. Если же площадь мембраны выходных веточек волокна больше, чем у той веточки, по которой приходит импульс, то ПД около точки ветвления замедляется и может даже заблокироваться.
В нейронах беспозвоночных в области узлов ветвления может возникать совсем иная ситуация. Дело в том, что у них, как уже говорилось, синапсы располагаются не на теле нейрона, а на разных веточках отростка нервной клетки, так что эти веточки могут возбуждаться независимо друг от друга. Представим себе узел ветвления, в котором две тонкие веточки и одна более толстая. Соотношение их диаметров может быть таким, что ПД не проходит в толстую веточку ни из одной тонкой, когда они возбуждаются по отдельности, но проходит в том случае, когда ПД возникает сразу в обеих тонких веточках и подходит к месту ветвления более или менее одновременно. Такой узел ветвления работает как схема совпадений или логический элемент «И»: импульс за узлом ветвления возникает только тогда, когда имеют место два события одновременно, и отсутствует, если возникает только одно из них. Нейроны, работающие по этому принципу, были действительно обнаружены у некоторых моллюсков.
С помощью узлов ветвления такого «логического» типа, в принципе, в нервной системе может быть образовано много разных устройств. Например, легко представить себе нейрон, который обнаруживает источник звука, расположенный прямо впереди животного;
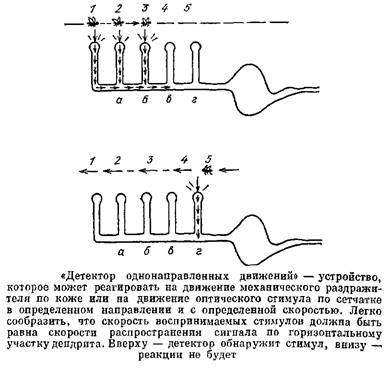
сигналы от него будут приходить к ушам одновременно. В качестве другого примера рассмотрим «детектор однонаправленных движений». Пусть имеется нейрон со структурой дендрита, как на рис. 45. Пусть на каждую его веточку действует, например, фоторецептор. Если световой стимул пробегает по фоторецепторам слева направо, то поочередно возбуждаются веточки 2, 2„ 3 и т. д. Когда ПД от веточки / приходит к первому узлу! туда же подходит сигнал от веточки 2г происходит их суммация, импульс преодолевает «логический» узел и идет дальше. У следующего узла встречаются этот импульс и ПД от веточки 3 и т. д. Если же стимул движется в противоположном направлении, то импульс от веточки 5 затухнет, так как к нему «на подмогу» не придет импульс от веточки 4.