Реферат: Применение обобщенного метода Фурье в задаче полого волновода треугольного сечения

Условие по оси х, имеющее вид f(x,0)=0, приводит к уравнению:

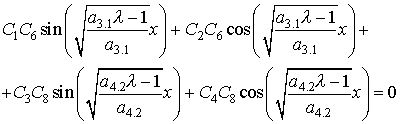(14),

из которого следует :

Условие по оси y, имеющее вид f(0,y)=0, приводит к уравнению:

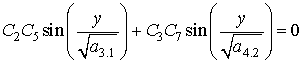(15),

из которого полагаем:

Условие по гипотенузе рассматриваемого треугольника, имеющее вид f(y-а,y)=0, приводит к уравнению:

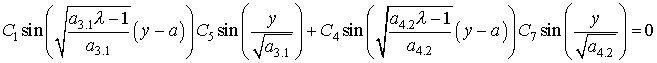
которое может быть преобразовано к виду:

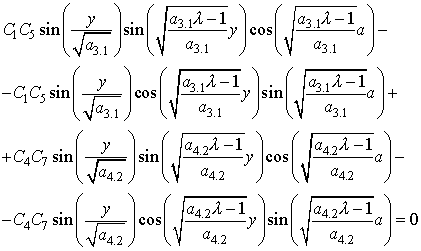(16)

Решая данное тригонометрическое уравнение можно обратить его в тождество при следующих ограничениях на неопределенные постоянные:

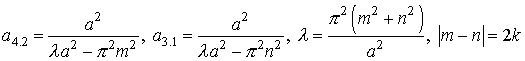(17),

где k,n,m v целые ненулевые числа.

При этих ограничениях искомая функция принимает следующий вид:

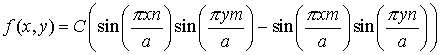(18),

где С v неопределенная амплитудная константа, появившаяся вследствие следующих обозначений:

Возвращаясь к первоначально поставленной задаче об определении семейства Е-волн рассматриваемой направляющей структуры, согласно [2], в качестве f(x,y) выступают собственные функции, имеющие смысл продольной компоненты напряженности электрического поля для волны, определяемой выбором чисел m и n. Этим собственным функциям соответствуют собственные значения из выражения (17). Полное электромагнитное поле для этого волновода может быть определено из зависимостей поперечных компонент от и, вытекающих из уравнений Максвелла:

,

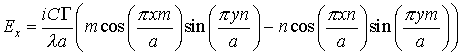
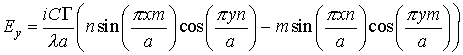
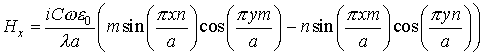
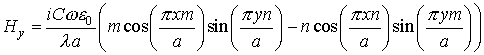где - продольное волновое число, а - круговая частота волнового процесса.

Список литературы

1. И.Е. Андрушкевич. Об одном обобщении метода Фурье разделения переменных. ЭВ & ЭС .1998. ¦2

2 В.В. Никольский, Никольская Т.И. Электродинамика и распространение радиоволн. М.: Наука.1989