Реферат: Призма и параллелепипед

|
Поскольку все грани параллелепипеда – параллелограммы, то прямая AD параллельна прямой ВС, а прямая ![]() параллельна прямой
параллельна прямой ![]() . Отсюда следует, что плоскости рассматриваемых граней параллельны.
. Отсюда следует, что плоскости рассматриваемых граней параллельны.
Из того, что грани параллелепипеда – параллелограммы, следует, что АВ, ![]() , CD и
, CD и ![]()
![]() параллельны и равны. Отсюда сделаем вывод, что грань
параллельны и равны. Отсюда сделаем вывод, что грань ![]() совмещается параллельным переносом вдоль ребра АВ с гранью
совмещается параллельным переносом вдоль ребра АВ с гранью ![]() . Следовательно, эти грани равны.
. Следовательно, эти грани равны.
2 ) Возьмем две диагонали параллелепипеда (рис. 5), например, ![]() и
и ![]() , и проведем дополнительные прямые
, и проведем дополнительные прямые ![]() и
и ![]() . АВ и
. АВ и ![]() соответственно равны и параллельны ребру DC, поэтому они равны и параллельны между собою; вследствии этого фигура
соответственно равны и параллельны ребру DC, поэтому они равны и параллельны между собою; вследствии этого фигура ![]() есть параллелограмм, в котором прямые
есть параллелограмм, в котором прямые ![]() и
и ![]() – диагонали, а в параллелограмме диагонали делятся в точке пересечения пополам. Аналогично мы можем доказать, что две другие диагонали пересекаются в одной точке и делятся этой точкой пополам. Точка пересечения каждой пары диагоналей лежит в середине диагонали
– диагонали, а в параллелограмме диагонали делятся в точке пересечения пополам. Аналогично мы можем доказать, что две другие диагонали пересекаются в одной точке и делятся этой точкой пополам. Точка пересечения каждой пары диагоналей лежит в середине диагонали ![]() . Таким образом, все четыре диагонали параллелепипеда пересекаются в одной точке О и делятся этой точкой пополам. Таким образом, точка пересечения диагоналей параллелепипеда является его центром симметрии. [3, 21]
. Таким образом, все четыре диагонали параллелепипеда пересекаются в одной точке О и делятся этой точкой пополам. Таким образом, точка пересечения диагоналей параллелепипеда является его центром симметрии. [3, 21]
Теорема:
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Доказательство:
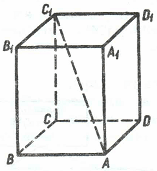
Это выплывает из пространственной теоремы Пифагора. Если ![]() – диагональ прямоугольного параллелепипеда
– диагональ прямоугольного параллелепипеда ![]() , то
, то ![]() – ее проекции на три попарно перпендикулярные прямые (рис. 6). Следовательно,
– ее проекции на три попарно перпендикулярные прямые (рис. 6). Следовательно, ![]() . [2, 116]
. [2, 116]
|
Замечание: в прямоугольном параллелепипеде все диагонали равны.
Дополнительные соотношения между элементами призмы
Если в наклонной призме боковое ребро ![]() образует одинаковые углы со сторонами основания, которые выходят из вершины
образует одинаковые углы со сторонами основания, которые выходят из вершины ![]() , то основание О высоты
, то основание О высоты ![]() лежит на биссектрисе угла
лежит на биссектрисе угла ![]() (рис. 7).
(рис. 7).
Доказательство: ![]()
|
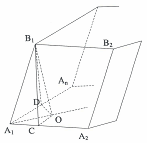
Проведем ![]()
![]() и отрезки
и отрезки ![]()
![]() Согласно теореме о трех перпендикулярах, имеем
Согласно теореме о трех перпендикулярах, имеем ![]() и
и ![]() . Прямоугольные треугольники
. Прямоугольные треугольники ![]() и
и ![]() равны, поскольку имеют общую гипотенузу
равны, поскольку имеют общую гипотенузу ![]() и одинаковые углы (
и одинаковые углы (![]() по условию). Следовательно,
по условию). Следовательно, ![]() и
и ![]() , отсюда
, отсюда ![]() Таким образом, точка О равноудалена от сторон угла
Таким образом, точка О равноудалена от сторон угла ![]() и, следовательно, лежит на биссектрисе
и, следовательно, лежит на биссектрисе ![]() угла
угла ![]() . [3, 24]
. [3, 24]
Задачи
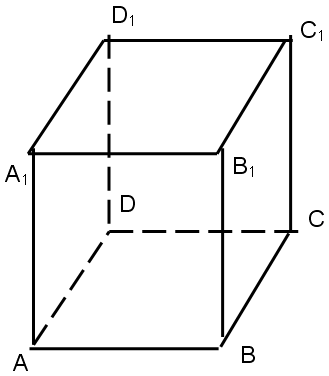
1. Ребро куба равно а.
Найдите:
Диагональ грани: d= a√2.
Диагональ куба: D= a√3.
Периметр основания: P= 4a.
2 . Основанием прямой призмы является равнобедренный треугольник, в котором высота проведенная к основанию равняется 8см. Высота призмы равняется 12см. Найдите полною поверхность призмы если боковая грань что содержит основание треугольника - квадрат.
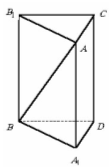
Решение
Площадь поверхности призмы будет равна сумме площадей оснований и сумме площадей боковых поверхностей, то есть ![]() , где
, где ![]() - площадь основания призмы,
- площадь основания призмы, ![]() - площадь боковой поверхности, содержащей основание,
- площадь боковой поверхности, содержащей основание, ![]() - площадь боковой поверхности, содержащей стороны равнобедренного треугольника. (Они равны, так как стороны основания равны в следствие того, что треугольник равнобедренный, а вторые стороны равны высоте призмы)
- площадь боковой поверхности, содержащей стороны равнобедренного треугольника. (Они равны, так как стороны основания равны в следствие того, что треугольник равнобедренный, а вторые стороны равны высоте призмы)
Поскольку боковая грань, содержащая основание треугольника, является квадратом, то основание треугольника также равно 12 см. (основание треугольника одновременно является стороной грани).
Таким образом, зная высоту и основание равнобедренного треугольника можно найти его остальные стороны и площадь:
![]()
Катеты, соответственно равны (у нас высота, являющаяся в равнобедренном треугольнике одновременно и медианой ![]() , с каждым из катетов образует прямоугольный треугольник) по теореме Пифагора:
, с каждым из катетов образует прямоугольный треугольник) по теореме Пифагора:
![]()
Таким образом: