Реферат: Проектирование манипулятора
Для определения параметров рабочей зоны необходимо рассчитать геометрические размеры манипулятора.
Следовательно, необходимо определить размеры цилиндра поступательного перемещения, а также размеры цилиндра вращательного перемещения.
 |
??????? ????????? ??????? ???????? ??????????????? ???????????:
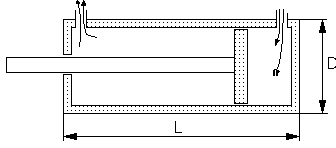
Рис.2 Цилиндр поступательной подвижности
Определим длину цилиндра L по формуле:
![]() , где
, где
Н – заданное поступательное перемещение
1,1 – взято из конструктивных соображений
![]()
Определим диаметр цилиндра D по формуле:
![]()
![]()

 |
????????? ??????? ???????? ???????????? ????????????:
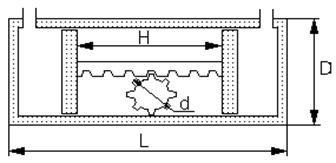
Рис.3 Цилиндр вращательной подвижности
Определим длину цилиндра L по формуле:
![]() , где
, где
Н – величина поступательного перемещения для поворота на необходимый угол, которая определяется по формуле Н = pd для поворота на угол 360°
d – диаметр вала вращения (4см)
0,05 – запас на поршни и другие конструктивные элементы
Так как имеется две вращательные подвижности, то была рассчитана длина каждой подвижности, которые равны:
![]()
![]()
Определим диаметр цилиндра D по формуле:
![]() , где
, где
2,5 – коэффициент, учитывающий диаметр вала вращения и тодлщину рейки
1,1 – из конструктивных соображений
Результаты определения диаметра:
![]()
![]()

 |
Рис.4 Параметры рабочей зоны
На рисунке 4 представлена рабочая зона рабочего органа. Из данного рисунка видно, что четыре точки позиционирования рабочего органа отмечены цифрами 1,2,3,4.

4. Упрощённая конструкция манипулятора со связанными системами координат
 |
Рис.5 Упрощённая конструкция манипулятора со связанными системами координат
Связанные системы координаты расставлены в соответствии с представлениями Денавита – Хартенберга.
Система [X0 ,Y0 ,Z0 ] – связанная система координат 1-го звена
[X1 ,Y1 ,Z1 ] – связанная система координат 2-го звена
[X2 ,Y2 ,Z2 ] – связанная система координат 3-го звена
[XР ,YР ,ZР ] – связанная система координат рабочего органа

5. Результирующие однородные матрицы преобразований для каждой точки позиционирования
Результирующие однородные матрицы преобразования определяются с помощью уравнения кинематики манипулятора:
![]()
 Определение однородной матрицы преобразования для первой точки позиционирования рабочего органа:
Определение однородной матрицы преобразования для первой точки позиционирования рабочего органа:
![]()
![]()