Реферат: Программная реализация модального управления для линейных стационарных систем

· Система с введенной обратной связью описывается уравнением

(3)

· Характеристическое уравнение системы (1) имеет вид

(4)

· Характеристическое уравнение системы (3) с задаваемыми (желаемыми) корнями имеет вид

(5)

Алгоритм:

1. Для исходной системы (1) составляем матрицу управляемости

2. Обращаем матрицу , т.е. вычисляем .

Если не существует (т.е. матрица - вырожденная), то прекращаем вычисления: полное управление корнями характеристического уравнения (5) не возможно.

3. Вычисляем матрицу

4. Составляем матрицу

5. Вычисляем матрицу, обратную матрице , т.е.

6. Вычисляем матрицу - матрицу в канонической форме фазовой переменной:

где - коэффициенты характеристического уравнения (4).

Матрица в канонической форме имеет вид

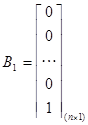
7. Составляем вектор , элементам которого являются коэффициенты характеристического уравнения (4), т.е. , ,

где - элементы матрицы .

8. Находим коэффициенты характеристического уравнения (5) (см. пояснения) и составляем из них вектор .

9. Вычисляем вектор .

- искомая матрица обратной связи системы (3), но она вычислена для системы, матрицы которой заданы в канонической форме фазовой переменной ( и ).

10. Для исходной системы (3) матрица обратной связи получается по формуле

Матрица - искомая матрица обратной связи.

Пояснения к алгоритму: