Реферат: Расчет параметров ступенчатого p-n перехода zip 860 kb

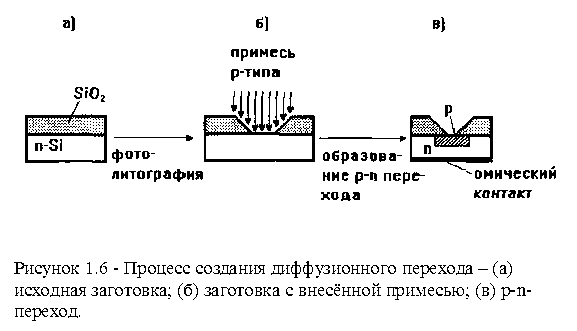
Диффузионные переходы получают диффузией примесного вещества в исходную полупроводниковую пластинку (рис. 1.6.). Это один из наиболее широко используемых методов получения p-n-перехода, он имеет несколько разновидностей.

При планарном методе диффузии переходы получают, используя изолирующий слой, препятствующий диффузии примесей. На поверхности кремния n-типа выращивается тонкий (около 3 мкм) слой двуокиси кремния SiO₂ (рис. 1.6.). Фотолитографическим методом в определенных местах окисла получают «окна», через которые диффундирующие примеси проникают в n-слой, образуя переход.

Методы диффузии обеспечивают получение плавных p-n переходов и используются при изготовлении интегральных микросхем.

1.3.4 Эпитаксиальные переходы .

Эпитаксиальные переходы образуются ориентированным направлением слоя монокристаллического полупроводника на исходном монокристалле-подложке (рис. 1.7.).

1–p-n-переход; 2–p-область; 3–слой высокоомного полупроводника; 4–подложка.

Рисунок 1.8 Эпитаксиальный переход, образованный по планарно-эпитаксиальному методу.

Для проведения эпитаксии необходимо создавать условия для конденсации атомов осаждаемого вещества на поверхности подложки. Конденсация происходит перенасыщением пара или жидкого раствора, а также при испарении осаждаемого вещества в вакууме в специальных реакторах. При наращивании плёнки с проводимостью противоположной подложке, образуется p-n-переход.

При изготовлении интегральных схем широко используют планарно-эпитаксиальный метод. Особенность такого технологического процесса заключается в том, что путём наращивания на подложку 4 из низкоомного кремния наносят тонкий слой 3 высокоомного полупроводника, повторяющего структуру подложки. Этот слой, называемый эпитаксиальным, покрывают плотной защитной пленкой SiO₂ толщиной 1 мкм (рис. 1.8.). В плёнке протравливают «окно», через которое путем диффузии бора или алюминия создается p-n-переход, выход которого на поверхность оказывается сразу же надежно защищенным пленкой окисла.

Следует отметить, что в последние годы широкое распространение получили такие методы формирования p-n-переходов, как ионное легирование и молекулярно-лучевая эпитаксия.

1.4 Энергетическая диаграмма p-n-перехода в равновесном состоянии.

Для анализа физических процессов, протекающих в полупроводниковых приборах удобно использовать метод энергетических диаграмм. Энергетическая диаграмма p-n-перехода в состоянии термодинамического равновесия представлена на рис. 1.9.

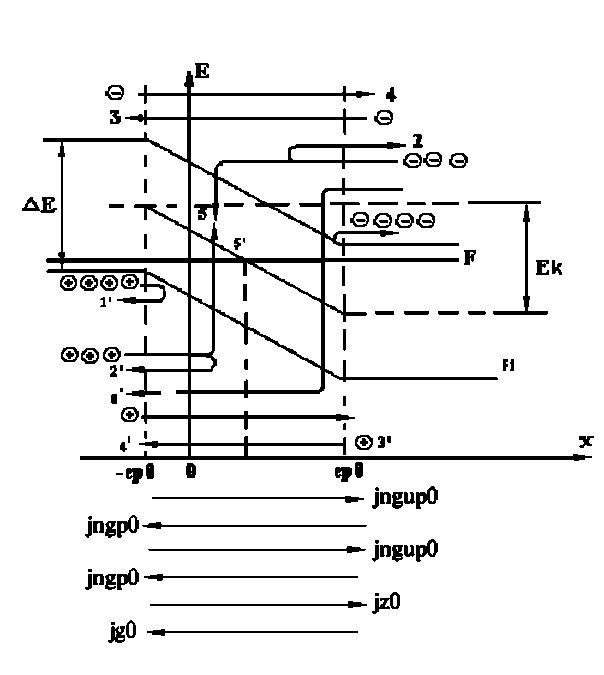Рисунок 1.9 Энергетическая диаграмма p-n перехода.

На оси ординат отложена энергия электрона Е. Энергия дырок на диаграмме возрастает в направлении - Е. Так как частицы стремятся занять состояние с минимальной энергией, электроны на диаграмме имеют тенденцию «утонуть», а дырки «всплыть». При отсутствии вырождения, общий для всей системы уровень Ферми расположен внутри запрещенной зоны, ширина которой не зависит от координаты. Уровень электростатической энергии F, показан на рис. 1.9. пунктиром, соответствует положению уровня Ферми в собственном полупроводнике и расположен вблизи середины запрещенной зоны. Энергетические уровни изображены горизонтальными прямыми. Это выражает тот факт, что энергия электрона, находящегося на данном уровне, например, на дне зоны проводимости, во всех точках полупроводника одинакова. После установления равновесия, образуется р-n–переход с потенциальным барьером для основных носителей равным j₀ = qV_k . Электроны, переходящие из n- в р–область, преодолевая этот барьер, увеличивают свою потенциальную энергию на j₀ = qV_k . Поэтому все энергетические уровни полупроводника, искривляясь в область p-n-перехода, поднимаются вверх на Е_к , как показано на рис. 1.9. При этом уровни Ферми F₀ и F устанавливаются на данной высоте, как в случае двух металлов.

В электрических нейтральных областях эмиттера (х<-l_р0 ) и базы (х>l_n0 ) поле равно нулю, и уровни Е_с (энергия, соответствующая дну зоны проводимости), Е_v (энергия, соответствующая потолку валентной зоны), F_i (электрическая энергия); располагаются горизонтально. В области p-n-перехода (-l_p0 <х<l_n0 ) электрическое поле направлено справа налево (вдоль градиента F_i ).

Равновесная концентрация носителей заряда в отсутствии вырождения определяется взаимным расположением уровней F и F_i .

n_о = n_i ехр [(F - F_i ) / kT ] (1.4.1)

p_о = n_i ехр [(F_i - F ) / kT ] (1.4.2)

В эмиттере p-типа (х<L_p0 ) фермиевская энергия меньше электрической энергии:F<F_i , p_р0 >n_р0

В базе n-типа: F > F_i , n_n0 >p_n0

В плоскости физического перехода Х-Х_ф выполняется условие:

F_i (X_ф ) =F

Ввиду искривления запрещенной зоны в области перехода между эмиттером и базой существует энергетический барьер, высота которого равна разности электростатических энергий в n- и p-областях (рис.1.9.).

Е_к =F_ip -F_in

Соответственно потенциалы эмиттера и базы отличаются на величину

φ_к =(F_ip - F_in )/e, (1.4.3)

где j_к - контактная разность потенциалов.

Энергетический барьер препятствует диффузионным потокам электронов из базы в эмиттер и дырок, из эмиттера в базу. Величина барьера автоматически становится такой, чтобы точно скомпенсировать диффузные потоки.

1.5 Токи через p-n-переход в равновесном состоянии.

Рассмотрим зонную диаграмму p-n-перехода. Градиенты концентрации подвижных носителей заряда, а также градиент электрического потенциала в p-n-переходе вызывает появления диффузионных и дрейфовых токов через переход. Механизм протекания токов представлен на рис. 1.9., где дырки изображены кружками со знаком «+», а электроны со знаком «–».