Реферат: Расчет параметров ступенчатого p-n перехода zip 860 kb

Электрическое поле может быть найдено из уравнения Пуассона:

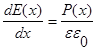(1.6.3)

При этом контактная разность потенциалов равна:

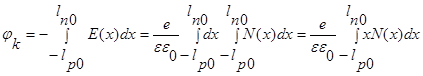
Поскольку функция P(x) меняет знак в точке X=0, а на границах перехода в поле равно нулю – напряженность электрического поля составляет:

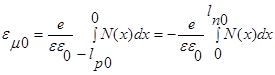(1.6.4)

Условие (1.6.4) соответствует электрической нейтральности p-n-перехода в целом:

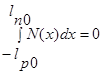(1.6.5)

Уравнения (1.6.2.б), (1.6.3), (1.6.5) могут быть решены относительно неизвестных l_{p 0} , и l_{n 0} , после чего из (1.6.4) определяется максимальное поле p-n-перехода.

1.7. Расчет параметров ступенчатого p-n-перехода.

Наиболее просто определяется параметры ступенчатого p-n-перехода, так как в этом случае функция N(x) имеет вид:

(1.7.1)

а значение граничных условий концентрации примеси и известны:

Контактная разность потенциалов определяется из уравнений (1.6.2.б)

;

;

;

Подставляя (1.7.1), (1.6.3), (1.6.5), с учетом очевидного соотношения , получим:

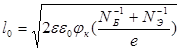(1.7.2)

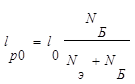
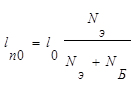
Максимальная напряженность электрического поля определяется из (1.6.4).

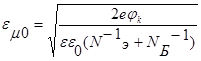
Из (1.7.2) следует, что при условии N_э >>N_Б практически весь переход сосредоточен в области базы (1_р0 <<1_n0 = 1₀ ).

Поскольку величина j_к слабо логарифмически зависит от концентрации примеси в эмиттере, при N_э >>N_Б параметры перехода определяются практически только свойством базы:

(1.7.3)

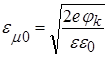
ЧАСТЬ II. Расчет контактной разности потенциалов j _k в p-n-переходе.

– контактная разность потенциалов, где: