Реферат: Расчет распределения примесей в кремнии при кристаллизационной очистке и диффузионном легировании
Расчет распределения сурьмы в кремнии будем производить аналогично расчету галлия в слитке кремния (пункт 1.2.1), при тех же условиях зонной плавки.
Переведем N0 в см-3 . Атомная масса сурьмы = 121,7
N0 =0,02 % (массовых) = 4,62×10-3 % (атомных) = 2,31×1018 см-3 .
Для расчета эффективного коэффициента сегрегации kэфф воспользуемся выражением (4). Для сурьмы в кремнии k0 =2,3×10-3 [1]. Отношение d/Dж =200 с/см из задания.
Подставляя значения k0 , d/Dж , Vкр в (4), вычислим kэфф . Для трех скоростей кристаллизации Vкр =2,5×10-3 ; 8,33×10-3 ; 2,5×10-2 см/с соответственно получим kэфф =3,74×10-2 ;0,11; 0,78.
Заполним расчетную таблицу.
Таблица 3 - Распределение сурьмы и удельного сопротивления вдоль слитка кремния после зонной плавки (один проход расплавленной зоной).
Участок зонной плавки | Участок направленной Кристаллизации | ||||
а | Nтв , см-3 | r , Ом×см (по кривым Ирвина) | g (a=10) | Nтв , см-3 | r , Ом×см (по кривым Ирвина) |
| Vкр =2,5×10-3 см/с | |||||
| 0 | 8,64 1016 | 0,11 | 0 | 7,22 1017 | 0,028 |
| 1 | 1,68 1017 | 0,075 | 0,2 | 8,95 1017 | 0,023 |
| 2 | 2,47 1017 | 0,052 | 0,4 | 1,18 1018 | 0,0215 |
| 3 | 3,22 1017 | 0,047 | 0,6 | 1,74 1018 | 0,0192 |
| 4 | 3,95 1017 | 0,04 | 0,8 | 3,4 1018 | 0,014 |
| 5 | 4,66 1017 | 0,038 | 0,9 | 6,62 1018 | 0,0082 |
| 6 | 5,33 1017 | 0,033 | 0,99 | 6 1019 | 0,00135 |
| 7 | 6 1017 | 0,031 | – | – | – |
| 9 | 7,22 1017 | 0,028 | – | – | – |
| Vкр =8,33×10-3 см/с | |||||
| 0 | 2,54 1017 | 0,051 | 0 | 1,55 1018 | 0,02 |
| 1 | 4,68 1017 | 0,038 | 0,2 | 1,89 1018 | 0,018 |
| 2 | 6,6 1017 | 0,03 | 0,4 | 2,44 1018 | 0,016 |
| 3 | 8,32 1017 | 0,027 | 0,6 | 3,5 1018 | 0,013 |
| 4 | 9,86 1017 | 0,024 | 0,8 | 6,49 1018 | 0,0085 |
| 5 | 1,12 1018 | 0,022 | 0,9 | 1,2 1019 | 0,0055 |
| 7 | 1,36 1018 | 0,0205 | 0,99 | 9,3 1019 | 0,00088 |
| 8 | 1,46 1018 | 0,02 | – | – | – |
| 9 | 1,55 1018 | 0,02 | – | – | – |
| Vкр =2,5×10- 2 см/с | |||||
| 0 | 1,8 1018 | 0,019 | 0 | 2,31 1018 | 0,0157 |
| 1 | 2,08 1018 | 0,017 | 0,2 | 2,42 1018 | 0,0156 |
| 2 | 2,2 1018 | 0,016 | 0,4 | 2,58 1018 | 0,015 |
| 3 | 2,26 1018 | 0,0158 | 0,6 | 2,82 1018 | 0,014 |
| 5 | 2,3 1018 | 0,0157 | 0,8 | 3,29 1018 | 0,0137 |
| 7 | 2,31 1018 | 0,0157 | 0,9 | 3,83 1018 | 0,012 |
| 9 | 2,31 1018 | 0,0157 | 0,99 | 6,36 1018 | 0,0086 |
 |
|
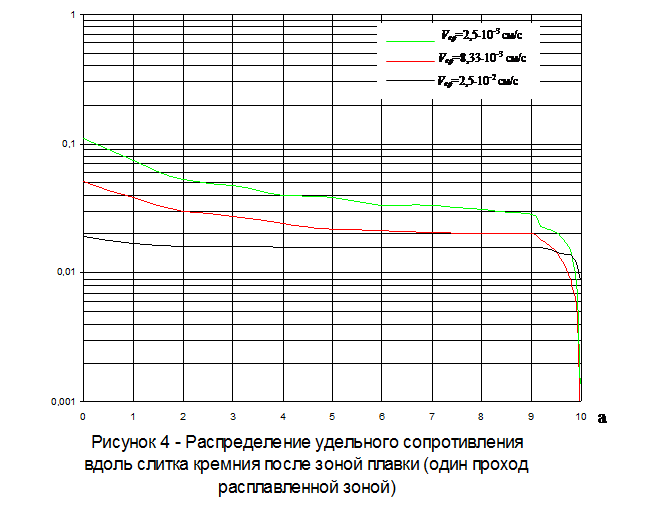На основании полученных данных построим графики распределения примесей вдоль слитка кремния после зонной плавки (один проход расплавленной зоной).
1.3. Распределение примесей после диффузии.
Основой математического описания процессов диффузии являются два дифференциальных уравнения Фика (немецкий ученый A. Fick предложил их в 1855 г.).
Первое уравнение (первый закон Фика) записывается следующим образом:
J = - D grad N (7)
где J - плотность потока диффундирующего вещества , т.е. количество вещества, проходящего за единицу времени через единичную площадь поверхности, перпендикулярной направлению переноса вещества;
N - концентрация атомов примеси.
D - коэффициент диффузии.
Физический смысл этого уравнения — первопричиной диффузионного массопереноса вещества является градиент его концентрации. Скорость переноса пропорциональна градиенту концентрации, а в качестве коэффициента пропорциональности вводится коэффициент диффузии. Знак минус в правой части (7) указывает на то, что диффузия происходит в направлении убывания концентрации. Другими словами, диффузия идет благодаря стремлению системы достичь физико-химического равновесия. Процесс будет продолжаться до тех пор, пока химические потенциалы компонентов всей системы не станут равными. Уравнение (7) описывает стационарный (установившийся) процесс - процесс, параметры которого не зависят от времени.
В макроскопическом представлении коэффициент диффузии определяет плотность потока вещества при единичном градиенте концентрации и является, таким образом, мерой скорости выравнивания градиента концентрации. Размерность коэффициента диффузии - м2 /с . В общем случае диффузия анизотропна и коэффициент диффузии - симметричный тензор второго ранга.
Согласно микроскопическому определению, компонента Dx коэффициента диффузии D по координате x связана со среднеквадратичным смещением 
диффундирующих атомов по координате x и интервалом времени Dt , в течение которого это смещение произошло соотношением
Когда концентрация вещества изменяется только в одном направлении (одномерная диффузия) и при диффузии в изотропной среде (коэффициент диффузии - скаляр) первое уравнения Фика имеет следующий вид:
(8)
При простейшем анализе структур и в простейших моделях процессов легирования в технологии изготовления ИМС предполагаются именно такие условия диффузии.
Второе уравнение диффузии (второй закон Фика) получается путем сочетания первого закона и принципа сохранения вещества , согласно которому изменение концентрации вещества в данном объеме должно быть равно разности потоков этого вещества на входе в объем и выходе из него.
В общем случае второе уравнение диффузии имеет следующий вид
(9)
Для одномерной диффузии в изотропной среде уравнение (9) можно записать
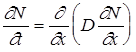(10)
Второй закон Фика характеризует процесс изменения концентрации диффундирующей примеси во времени в различных точках среды и является математической моделью нестационарного (развивающегося) состояния системы (описывает период времени от начала процесса до установления стационарного состояния).
При постоянстве коэффициента диффузии D (независимости его от концентрации примеси) уравнение (10) упрощается
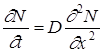(11)
Допущение о постоянстве коэффициента диффузии справедливо в большом количестве случаев, анализируемых в технологии ИМС.
Уравнения диффузии являются чисто феноменологическими, т.е. они не содержат никаких сведений о механизмах диффузии - о диффузионном процессе на атомном, уровне. Кроме того, уравнения (7) - (11) не содержат информации о зарядовом состоянии диффундирующих частиц.
Процессы диффузии, используемые для изготовления интегральных структур, обычно анализируются с помощью частных решений уравнения (11) т.к., в отличие от (8), именно оно содержит важный параметр - время установления некоторого анализируемого состояния системы. Основная цель решения уравнения - найти распределение примеси N(x,t) в полупроводнике после диффузии в течение определенного времени t при различных условиях осуществления процесса.
Общее решение уравнения (11) для бесконечного твердого тела при заданном в общем, виде начальном распределении примеси N(x,0) = f(x) может быть найдено методом разделения переменных. Оно имеет вид
, (12)