Реферат: Расчет распределения примесей в кремнии при кристаллизационной очистке и диффузионном легировании

Бесконечным в одномерном представлении называют тело, простирающееся от x=0 до x=- ¥ и до x=+ ¥ .

Часто при поиске распределения концентрации примеси в полупроводнике необходимо решение уравнения (11) для полубесконечного твердого тела. Полубесконечным в одномерном представлении называют тело, простирающееся от x=0 до x=+ ¥ .

Для этого случая выражение (12) может быть приведено к виду

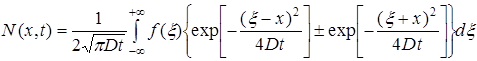(13)

В выражении (13) знак плюс относится к ситуации, когда граница твердого тела (x=0) является непроницаемой для диффундирующего вещества, находящегося в области x>0, (отражающая граница ), а знак минус - к случаю, когда на границе твердого тела в любой момент времени концентрация диффундирующего вещества, также находящегося в области x>0, равна нулю - связывающая граница .

Представленные решения позволяют находить распределения примеси в твердом теле при любых начальных условиях. Решение конкретной задачи сводится к подстановке в (12) или (13) соответствующих ситуации начальных условий с последующими, как правило, очень громоздкими преобразованиями.

1.3.1 Распределение примеси при диффузии из полубесконечного пространства (диффузия из концентрационного порога)

Диффундирующая примесь (диффузант ) поступает в полубесконечное тело через плоскость x=0 из второго полубесконечного тела (источника ) с равномерным распределением примеси. Концентрация примеси в источнике - N_o . Полагается, что в принимающем диффузант теле нет рассматриваемой примеси.

Начальное распределение концентраций для этого случая задается в виде

N(x,0) = N_o для x<0

N(x,0) = 0 для x>0

Решением уравнения (11) для этого случая является выражение

(14)

Второе слагаемое в квадратных скобках называют интегралом ошибок Гаусса или, иначе, функцией ошибок - error function и сокращенно обозначают erf (z). В соответствии с сокращением это распределение называют erf - распределением .

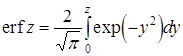(15)

В математике часто используют как самостоятельную и другую функцию

erfc z = 1- erf z (16)

которая называется дополнением функции ошибок до единицы или дополнительной функцией ошибок - error function complement. Обе функции табулированы.

Таким образом, выражение (14) можно записать

(17)

Величинаимеет размерность длины и носит название диффузионной длины или длины диффузии. Физический смысл этого параметра - среднее расстояние, которое преодолели диффундирующие частицы в направлении выравнивания градиента концентрации за время t.

Рассмотренное решение можно использовать как простейшую модель, представляющую распределение примеси в автоэпитаксиальной структуре. При этом, в качестве независимых источников примеси выступает как подложка, так и эпитаксиальный слой. Процессы диффузии с каждой стороны рассматриваются в этом случае как независящие друг от друга, а реальное распределение примесей на границе раздела будет представлять собой сумму отдельных решений.

1.3.2 Распределение примеси при диффузии из постоянного источника в полубесконечное тело.

Диффузант поступает в полубесконечное тело через плоскость x=0 из источника, обеспечивающего постоянную концентрацию примеси N_o на поверхности раздела твердое тело - источник в течение любо?