Реферат: Разработка методов анализа деформаций подземных сооружений

В таком случае ошибка дирекционного угла полигонометрического хода, учитывая, что поправка в угол вводится со знаком, обратным поперечному сдвигу, равна:

С учетом (3) получаем:

. (4)

Переходя от истинных ошибок измерения к средним квадратическим, для равноточно измеренных углов хода, произведя суммирование (4), имеем:

.

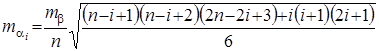На рис.2 показан характер изменения ошибки дирекционного угла вытянутого полигонометрического хода при количестве сторон 6, 8 и 10. Общей и необычной характеристикой полигонометрического хода, не имеющего примычных углов, является то, что наиболее точно определяется дирекционный угол в середине хода. На рис.2 приведены графики коэффициента k:

, где .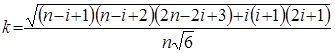

?????? ????????????? ???????????? ???????????????????? ????, ???????????? ?????? ?? ??? ?????? ? ?????????? ????????????, ??????????? ? ???, ??? ??? ????????? ?????????? ???????? ?????? ????????? ????????, ??? ??????? ????? ???? ????????? ?????????? "???????????" ????????????????-???? ????. ???????? ???????? ?????? ??????? ?????????? ????? ??? ?????? ????? ???????? ???????????????????? ???? ? ????????? ?? ? ???????????.

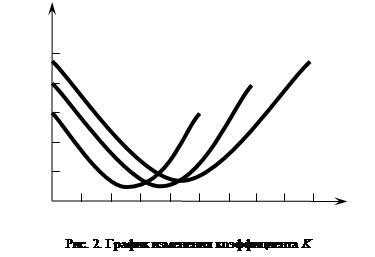Средняя квадратическая ошибка определения дирекционного угла в середине подземного полигонометрического хода, обусловленная ошибками угловых измерений, практически равна средней квадратической ошибке измерения углов. При количестве сторон в подземном полигонометрическом ходе не более 10, и средней квадратической ошибке измерения угла 2-3", основной ошибкой может стать ошибка передачи координат в тоннель. В диссертации выполнен подробный анализ точности определения координат пунктов подземной полигонометрической сети.

Выполненный анализ точности показывает, что подземный полигонометрический ход, опирающийся на два пункта, вполне может обеспечить точность, необходимую для наблюдения за изменением положения тоннеля. Основным недостатком данного метода является слабый контроль возможных промахов при выполнении работ.

В таких условиях геодезические работы необходимо выполнять особенно тщательно, обеспечив повторные измерения, для надлежащего контроля.

ГЛАВА 3. АНАЛИЗ ДЕФОРМАЦИЙ КОЛЕЦ ТОННЕЛЯ

Внедрение в геодезию современных средств измерений привело к появлению новых задач. Такой задачей является обработка спутниковых результатов измерений, когда встает вопрос об учете ошибок исходных данных. Если использовать основную формулу метода наименьших квадратов в традиционной записи:

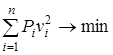,(5)

то возникает новая проблема: как вычислить веса параметров уравнений Кеплера и поправочных коэффициентов?

Для этой задачи сформулирована новая целевая функция: минимум суммы квадратов остаточного рассогласования преобразованных координат и координат государственной или местной системы координат. Формулировка целевой функции отличается от целевой функции, предложенной Гауссом при разработке метода наименьших квадратов. При использовании новой целевой функции можно достичь желаемого результата и вычислить параметры преобразования, но при этом возникают две очень сложные проблемы:

· как вычислить веса величин, используемых в обработке;

· как выполнять оценку точности параметров преобразования и преобразованных координат, так как Гаусс разработал метод оценки точности для другой целевой функции.

К этому же классу задач относится и методика анализа деформаций колец тоннеля. Современные алгоритмы обработки результатов измерений предусматривают вычисление положения вероятнейшей окружности под условием минимума суммы квадратов расхождений реального положения колец тоннеля от вероятнейшего. Новая целевая функция не позволяет использовать при обработке результатов измерений все точностные характеристики измеренных и приближенно известных величин и выполнить объективную оценку как результатов измерений, так и их функций.

С развитием дальномерной техники в геодезии стали широко применять полигонометрию и линейно-угловые сети. При уравнивании таких сетей возникли трудности: как вычислять веса для угловых и линейных измерений? Вес – величина размерная или безразмерная? Этот вопрос станет понятен, если целевую функцию (5) записать в виде:

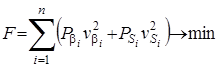,(6)

где – веса угловых измерений; – поправки в угловые измерения; – веса линейных измерений; – поправки в линейные измерения.

Если вес – величина безразмерная, то в целевой функции (6) будут складываться, например, квадратные секунды с квадратными миллиметрами. В результате остро стоит вопрос о соотношении весов в угловых и линейных измерениях. Для того чтобы устранить возникшую парадоксальную ситуацию, можно записать формулу (6) в следующем виде:

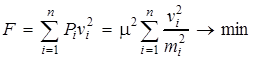. (7)

Средняя квадратическая ошибка единицы веса μ2, стоящая перед знаком суммы, не влияет на отыскание минимума, следовательно, целевую функцию (7) можно представить в окончательном виде:

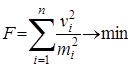. (8)

По сути, эта та же формула Гаусса, лишь записана она в другом виде. Однако такая форма записи снимает все трудности поиска соотношения весов между разнородными измерениями, так как под знаком суммы стоят безразмерные коэффициенты, если средние квадратические ошибки и поправки вычислены в единой размерности. Более того, целевая функция (8) позволяет вычислять поправки в любые величины, которые измерены или известны приближенно при совместной их обработке. В целевой функции (8) роль веса выполняет величина, обратная квадрату средней квадратической ошибки, что и рекомендовал Гаусс. Вводить в эту целевую функцию понятие веса бессмысленно, так как при обработке результатов измерений это ничего нового не прибавит и не убавит.

Аналогичная ситуация сложилась и при анализе результатов наблюдений за деформациями колец туннеля. По результатам угловых и линейных измерений вычисляют координаты нескольких точек по периметру тоннеля в условной системе координат, а затем вычисляют положение аппроксимирующей окружности под условием:

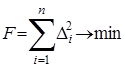, (9)

где Δi– отклонение радиуса аппроксимирующей окружности от реального расстояния от оси тоннеля до обделки.