Реферат: Решение дифференциальных уравнений 1 порядка методом Эйлера

Предположим, нам известны приближенные значения функции u ( x ) в k точках (стартовые k точек, в частности, можно найти методом Эйлера или методом Рунге-Кутта того или иного порядка), тогда функцию f ( x , u ( x )) в (2.4.2) для приближенного вычисления интеграла можно заменить на интерполяционный полином порядка k -1, построенный поk точкам , интеграл от которого считается явно и представляет собой линейную комбинацию значений cнекоторыми множителями . Таким образом, мы получаем следующую рекуррентную процедуру вычисления приближенных значений функции u ( x ) (являющимся точным решением задачи Коши) в точках :

(2.4.3)

Описанная схема является k - шаговой явной формулой Адамса.

Неявная схема Адамса.

Пусть - интерполяционный полином порядка k , построенный по k +1 значению б одно из которых, именно , мы будем считать неизвестным. Модифицируем (2.4.3), заменив в нём на полином более высокой степени , интеграл от которого выражается в виде линейной комбинации значений с некоторыми новыми коэффициентами :

(2.4.4)

Формула (2.4.4) представляет собой неявную схему Адамса и является уравнением на , которое можно решать методом последовательных приближений. Естественно, что начальное приближение , должно быть разумно выбрано. Для этого удобно объединить явную и неявную схемы Адамса в одну, называемую «методом коррекции». Именно с помощью явной схемы определяется начальное приближение (прогноз), а затем по неявной схеме оно необходимое число раз (обычно один или два) корректируется методом последовательных приближений до достижения заданной точности (коррекция).

2.5.Метод Эйлера.

Решить дифференциальное уравнение у^/ =f(x,y) численным методом - это значит для заданной последовательности аргументов х₀ , х₁ …, х_n и числа у₀ , не определяя функцию у=F(x), найти такие значения у₁ , у₂ ,…, у_n , что у_i =F(x_i )(i=1,2,…, n) и F(x₀ )=y₀ . (2.5.1)

Таким образом, численные методы позволяют вместо нахождения функции

У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k -x_k-1 называется шагом интегрирования.

Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Рассмотрим дифференциальное уравнение первого порядка (2.5.1)

с начальным условием

x=x₀ , y(x₀ )=y₀ (2.5.2)

Требуется найти решение уравнения (2.5.1) на отрезке [а,b].

Разобьем отрезок [a, b] на n равных частей и получим последовательность х₀ , х₁ , х₂ ,…, х_n , где x_i =x₀ +ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.

В методе Эйлера приближенные значения у(х_i )»y_i вычисляются последовательно по формулам у_i +hf(x_i , y_i ) (i=0,1,2…).

При этом искомая интегральная кривая у=у(х), проходящая через точку М₀ (х₀ , у₀ ), заменяется ломаной М₀ М₁ М₂ … с вершинами М_i (x_i , y_i ) (i=0,1,2,…); каждое звено М_i M_{i +1} этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения (2.5.1), которая проходит через точку М_i . Если правая часть уравнения (2.5.1) в некотором прямоугольнике R{|x-x₀ |£a, |y-y₀ |£b}удовлетворяет условиям:
|f(x, y₁ )- f(x, y₂ )| £N|y₁ -y₂ | (N=const), (2.5.3)

|df/dx|=|df/dx+f(df/dy)| £ M (M=const),

то имеет место следующая оценка погрешности:

|y(x_n )-y_n | £hM/2N[(1+hN)ⁿ -1], (2.5.4)

где у(х_n )-значение точного решения уравнения (2.5.1) при х=х_n , а у_n - приближенное значение, полученное на n-ом шаге.

Формула (13) имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет : сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагомh/2. Погрешность более точного значения у_n ^* оценивается формулой

|y_n -y(x_n )|»|y_n ^* -y_n |.(2.5.5)

Метод Эйлера легко распространяется на системы дифференциальных уравнений и на дифференциальные уравнения высших порядков. Последние должны быть предварительно приведены к системе дифференциальных уравнений первого порядка.

Модифицированный метод Эйлера

Рассмотрим дифференциальное уравнение (2.5.1) y^/ =f(x,y) с начальным условием y(x₀ )=y₀ . Разобьем наш участок интегрирования на n равных частей. На малом участинтегральную кривую заменим прямой линией.

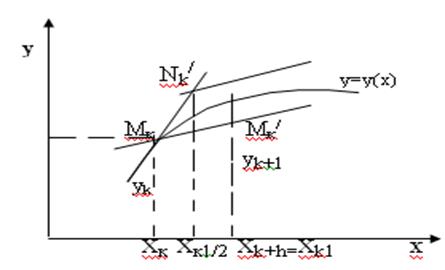
Рис.1 Метод Эйлера в графическом видa

Получаем точку М_к (х_к ,у_к ). Через М_к проводим касательную: у=у_к =f(x_k ,y_k )(x-x_k ). Делим отрезок (х_к ,х_к1 ) пополам:

x_Nk ^/ =x_k +h/2=x_{k +1/2 (2.5.6)}

y_Nk ^/ =y_k +f(x_k ,y_k )h/2=y_k +y_{k +1/2}