Реферат: Решение дифференциальных уравнений 1 порядка методом Эйлера
y(xk +1/2 )=f(xk +1/2 , yk +1/2 )=αk (2.5.7)
Из точки Мк проводим прямую с угловым коэффициентом αк и определяем точку пересечения этой прямой с прямой Хк1 . Получаем точку Мк / . В качестве ук+1 принимаем ординату точки Мк / . Тогда:
ук+1 =ук +αк h
xk +1 =xk +h
(2.5.8)αk =f(xk + h/2 , yk +f(xk ,Yk )h/2)
yk =yk -1 +f(xk -1 ,yk -1 )h
(2.5.8)-рекурентные формулы метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции ук+1/2 в точках хк+1/2 , затем находят значение правой части уравнения (11) в средней точке y/ k+1/2 =f(xk +1/2 , yk +1/2 ) и определяют ук+1 .
Для оценки погрешности в точке хк проводят вычисления ук с шагом h, затем с шагом 2h и берут 1/3 разницы этих значений:
| ук * -у(хк )|=1/3(yk * -yk ),(2.5.9)
где у(х)-точное решение дифференциального уравнения.
Таким образом, методом Эйлера можно решать уравнения любых порядков. Например, чтобы решить уравнение второго порядка y// =f(y/ ,y,x) c начальными условиями y/ (x0 )=y/ 0 , y(x0 )=y0 , выполняется замена:
y/ =z (2.5.10)
z/ =f(x,y,z)
Тем самым преобразуются начальные условия: y(x0 )=y0 , z(x0 )=z0 , z0 =y/ 0 . (2.5.12)
3.Описание алгоритмов решения задачи
3.1.Описание переменных.
| Наименование | Тип | Описание |
| Входные данные | ||
| Xi | double | Начальное значение (x) интервала вычисления |
| Xkon | double | Конечное значение (x) интервала вычисления |
| n | integer | Количество шагов |
| Yi | double | Начальное значение y |
| kx | double | Коэффициент при переменой x |
| ky | double | Коэффициент при переменной y |
| Выходные данные | ||
| h | double | Фиксированное приращение аргумента (x) |
| res | double | Расчётное значение уравнение y’=F(x,y) в точке (x) |
| Промежуточные | ||
| i | integer | Счётчик цикла |
| Yprom | double | Промежуточное значение y в точке Xprom |
| Xprom | double | Промежуточное значение x при h/2 |
| a | double | Решение уравнения в точках f(Xprom,Yprom) |
| f1 | double | Функция f(x,y) |
3.2. Блок- схема главного модуля
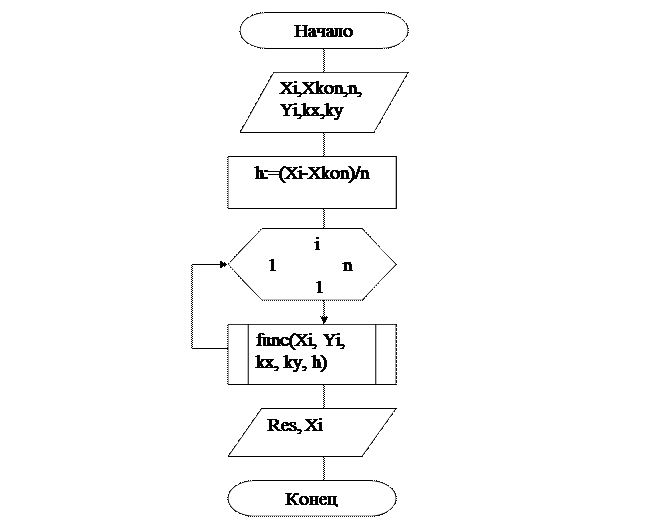
3.3 Описание алгоритма главной программы.
| Номер блока | Описание |
| 1 | Ввод начального и конечного значений интервала вычисления уравнения, количество шагов, начальное значение у, а также коэффициенты при kxи ky. |
| 2 | Вычисление фиксированного приращения аргумента х |
| 3 | Цикл с шагом 1 и конечным значением не превышающим количество шагов, который высчитывает значение yна определённом интервале |
| 4 | Функция для расчёта уравнения вида y’=f(x,y); |
5 |
Вывод результатов на интервале X |
3.4 Блок-схема функции “func”.
 3.5 Описание блок- схемы функции “func”.
3.5 Описание блок- схемы функции “func”.
Номер блока | Описание |
| 1 | Вычисление: функции f1 с подстановкой начальных значений; промежуточных значений Yprom и Xprom, значения aдля вычисления f(Xprom,Yprom) и расчёт результатов функции и переход на следующий шаг. |
| 2 | Приращение аргумента xна h |
| 3 | Вывод результатов уравнения и интервала |
*Реализация алгоритма на языке программирования C++ представлена в приложении .
4.Описание программного обеспечения.
4.1 Описание операционной системы
Основное требование к операционной системе (ОС), предъявляемое поставленной задачей, это наличие ANSI или POSIX совместимого компилятора языка C++.
Для реализации задачи была выбрана последняя клиентская версия операционной системы Microsoft, основанная на ядре NT – MicrosoftWindowsXPProfessional.
Указанная операционная система обладает рядом преимуществ:
· наличие достаточного количество ANSI или POSIX совместимых компиляторов языка C++, разработанных для данной ОС, а именно –
o Microsoft C++ (version 2-6)
o gcc
o Borland C++
o Intel C++
o прочие;
· достаточная управляемость, надежность и безопасность;
· широкое распространение основанных на ядре NT операционных систем Microsoft, совместимых по программному обеспечению с WindowsXPProfessional (NT/2000/XP/2003 – client & server);