Реферат: Решение уравнений в конечных разностях
![]()
Где p - некоторый параметр-константа. Количество частных решений определится числом параметров ![]() , для которых
, для которых ![]() будет обращать разностное уравнение в тождество. Общее решение составляется в виде суммы частных решений, умноженных на коэффициенты, определяемые конкретными начальными условиями. Рассмотрим пример решения линейного неоднородного уравнения третьего порядка.
будет обращать разностное уравнение в тождество. Общее решение составляется в виде суммы частных решений, умноженных на коэффициенты, определяемые конкретными начальными условиями. Рассмотрим пример решения линейного неоднородного уравнения третьего порядка.
Пусть требуется заменить рекуррентный вычислительный процесс с псевдокодом следующего вида:
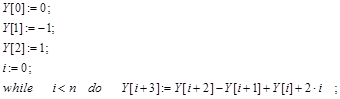
на формульное выражение для ![]() , как функции от n, позволяющее выборочно вычислять значение любого члена последовательности. Для этого в рекуррентном операторе цикла заменим оператор ': =' на символ равенства '=' и запишем полученное уравнение в форме неоднородного разностного уравнения относительно
, как функции от n, позволяющее выборочно вычислять значение любого члена последовательности. Для этого в рекуррентном операторе цикла заменим оператор ': =' на символ равенства '=' и запишем полученное уравнение в форме неоднородного разностного уравнения относительно ![]() :
:
![]() .
.
В качестве фундаментальной системы функций возьмем ![]() тогда характеристическое уравнение примет следующий вид:
тогда характеристическое уравнение примет следующий вид:
![]() .
.
Решив уравнение, найдем корни: ![]() , следовательно, частными решениями однородного уравнения будут:
, следовательно, частными решениями однородного уравнения будут:
![]()
Частное решение неоднородного уравнения (с правой частью) попробуем найти в виде функции, которая будет пропорциональна квадратуре от правой части с неизвестными коэффициентами:
![]()
Для нахождения коэффициентов a и b подставим в уравнение ![]() и приравняем коэффициенты при одинаковых степенях n в левой и правой частях полученного равенства. Последовательно выполняя сказанное, имеем:
и приравняем коэффициенты при одинаковых степенях n в левой и правой частях полученного равенства. Последовательно выполняя сказанное, имеем:

Раскрыв скобки и сгруппировав слагаемые при различных степенях n , получим
![]()
откуда![]() и частное решение примет вид
и частное решение примет вид
![]() .
.
Общее решение для конкретных начальных условий ищем в виде суммы частных решений:
![]() .
.
Константы ![]() находим из уравнений, получаемых после подстановки в общее решение значений для
находим из уравнений, получаемых после подстановки в общее решение значений для ![]() при
при ![]() :
:
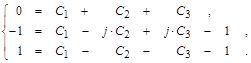
![]()
В результате, общее решение неоднородного уравнения будет:
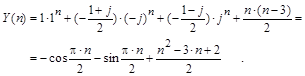
Для примера выпишем несколько первых членов ряда, полученных вычислением этого выражения: [0, - 1, 1, 2, 2, 5, 11, 16, 20, 27, 37, 46, 54, 65, 79, 92, 104, 119, 137, 154, 170,...]
3. Рекуррентные формулы для решения разностных уравнений
Интегрирование системы нелинейных разностных уравнений первого порядка по Эйлеру аналитически выполнить, как правило, не удается. Поэтому решение задачи получают в численном виде путем вычисления очередных значений процессов по рекуррентным формулам, начиная с известных начальных условий:
![]() ,
,
Где ![]() - очередное значение вектора решений,
- очередное значение вектора решений,