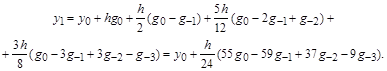Реферат: Решение уравнений в конечных разностях

Построение такого интерполяционного многочлена удобно осуществлять с применением повторных конечных разностей “назад”:

.

Взаимосвязь оператора и рассмотренных выше операторов и характеризуется следующими соотношениями:

Выразим ординату функции, отстоящую от текущей на k шагов назад, через ординату функции в текущей точке и выполним ряд эквивалентных преобразований с названными линейными операторами:

Если положить

, то

Таким образом, интерполяционный многочлен Ньютона для интерполирования “назад” принимает вид:

,

где принимает целые значения для ,

- i- тая повторная конечная разность “вперед", вычисляемая по значениям функции в соответствии с таблицей:

-4
-3						-
-2					-	-
-1				-	-	-
0				-	-	-
1				-	-	-

В таблице жирным шрифтом выделены конечные разности от нулевого порядка и выше, которые входят в интерполяционную формулу Ньютона.

4.2 Рекуррентные формулы Адамса

Пусть теперь требуется найти решение уравнения

.

для которого уже каким-либо способом найдены k +1 значений решения , что, естественно, определяет и соответству-ющие значения . На основе построим интерполя-ционный многочлен k- той степени:

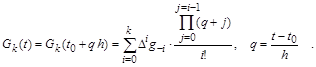
Приращение решения на внешнем интервале можно получить, проинтегрировав интерполяционный многочлен в интервале по переменной q , предварительно сделав замену переменных:

.

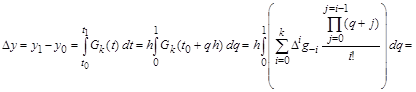
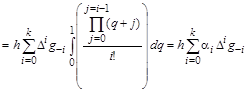Интегралы в каждом слагаемом зависят только от i и определяют коэффициенты, с которыми повторные разности входят в выражение для приращения. Таким образом, экстраполяционная формула Адамса имеет вид:

,

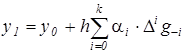где первые пять коэффициентов приведены в таблице

i	0	1	2	3	4

Появление нового значения требует для очередного шага вычислить новые значения повторных разностей. Для этого в таблице разностей заполняется по одной дополнительной клеточки в каждом столбце после одного-единственного вычисления правой части. В этом и состоит основное достоинство экстраполяционных формул.

В формулу Адамса вместо повторных разностей можно подставить их выражения через ординаты . Например, ограничившись , получим