Математика / Реферат: Решение задач по прикладной математике

Реферат: Решение задач по прикладной математике

P_6(2) = C_6(2) 0.8² (1-0.8)^(6-2) = 15 0.64 0.2⁴ = 0.01536

4. C_6(3) = = = = 20

P_6(3) = C_6(3) 0.8³ (1-0.8)^(6- ³ ⁾ = 20 0.512 0.2³ = 0.08192

P = P_6(0) + P_6(1) + P_6(2) + P_6(3) = 0.000064 + 0.001536 + 0.01536 + 0.08192 = = 0. 09888 0.099 - вероятность того, что к установленному сроку счета не оплатят не более трех потребителей.

Задание 2 . Найти среднее квадратическое отклонение вариационного ряда.

X₁ 800 1000 1200 1400 1600 1800 2000

n₁ 1 8 23 39 21 6 2

Среднее квадратическое отклонение случайной величины X вычисляется по формуле F_x = , где – дисперсия случайной величины X.

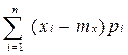
- математическое ожидание случайной величины X.

800 1 + 1000 8 + 1200 23 + 1400 39 + 1600 21 + 1800 6 + 2000 2 = 139400

= (800 - 139400) 1 + (1000 - 139400) 8 + (1200 - 139400) 23 + (1400 - -139400) 39 + (1600 - 139400) 21 + (1800 - 139400) 6 + (2000 - 139400) 2 =

= 19209960000 + 153236480000 + 439282520000 + 742716000000 + 398765640000 + + 113602560000 + 37757520000 = 1904570680000

F_x = 1380062

Задание 3 . Решить задачу линейного программирования симплексным методом.

Для производства двух видов изделий используются три вида сырья, запасы которого ограничены. Величины запасов приведены в матрице С. Нормы расхода сырья каждого вида на каждое из двух изделий приведены в матрице А , где строки соответствуют виду сырья, а столбцы – виду изделия. Прибыль от реализации изделий указана в матрице P.

Составить план производства изделий так, чтобы предприятие получило максимальную прибыль от их реализации.

5 9 7710