Реферат: Решение задачи линейного программирования симплекс-методом

Подлежит максимизации или минимизации.

Система ограничений в виде равенств и неравенств образует выпуклое множество - выпуклый многогранник. Это множество может быть ограниченным и неограниченным. Целевая функция задачи линейного программирования также является выпуклой функцией. Таким образом, задача линейного программирования является частным случаем задачи выпуклого программирования.

Рассмотрим систему ограничений задачи линейного программирования в виде равенств

(1)

Система (1) линейных уравнений совместна, если она имеет, по крайней мере, одно решение. Система (1) называется избыточной, если одно из уравнений можно выразить в виде линейной комбинации остальных.

В системе (1) число переменных (неизвестных n больше, чем число ограничений m. Будем считать, что ранг этой системы равен m (система неизбыточна) и что система (1) совместна. Тогда m переменных из общего их числа образуют базисные переменные, а остальные переменных называют небазисными. Если система уравнений имеет решение, то она имеет и базисное решение. Решение системы уравнений (1) называют допустимым, если все его компоненты неотрицательны. Если система линейных уравнений обладает допустимым решением, то она имеет и базисное допустимое решение. Совокупность всех допустимых решений системы (1) есть выпуклое множество, т.е. множество решений задачи линейного программирования выпукло. Так как это множество образовано плоскостями (гиперплоскостями), то оно имеет вид выпуклого многогранника. Базисное допустимое решение соответствует крайней точке выпуклого многогранника (его грани или вершине). Если существует оптимальное решение задачи линейного программирования, то существует базисное оптимальное решение.

Целевая функция задачи линейного программирования есть уравнение плоскости (или гиперплоскости для числа переменных больше трех). Максимальное или минимальное значение целевая функция задачи линейного программирования достигает либо в вершине выпуклого многогранника, либо на одной из его граней. Таким образом, решение (решения) задачи линейного программирования лежит в вершинах выпуклого многогранника и для его нахождения надо вычислить значения целевой функции в вершинах выпуклого многогранника, определяемого условиями-ограничениями задачи.

Решение задачи линейного программирования графическим методом.

Трудность построения математической модели заключается в идентификации переменных и последующем представлении цели и ограничений в виде математических функций этих переменных. Если модель содержит только две переменные, то задачу линейного программирования можно решить графически. В случае трёх переменных графическое решение становится менее наглядным, а при большем значении переменных – даже невозможным. Однако графическое решение позволяет сделать выводы, которые служат основой для разработки общего метода решения задачи линейного программирования.

Первый шаг при использовании графического метода заключается в геометрическом представлении допустимых решений, т.е. построении области допустимых решений (ОДР.), в которой одновременно удовлетворяются все ограничения модели. При получении графического решения переменная откладывается по горизонтальной оси, а – по вертикальной. При формировании ОДР необходимо предотвратить получение недопустимых решений, которые связаны с необходимостью выполнения условия неотрицательности переменных. Перед построением необходимо определить квадранты, в которых будет располагаться ОДР. Квадранты определяются знаками переменных и . Условия неотрицательности переменных и ограничивают область их допустимых значений первым квадрантом. Если переменная не ограниченна в знаке, то область ограничивается первым и вторым квадрантом, если , то – первым и четвёртым квадрантом. Другие границы пространства решений на плоскости , изображены прямыми линиями, построенными по уравнениям ограничений при условии замены знака на знак "=". При этом необходимо учитывать следующее: правые части всех ограничений должны быть неотрицательными . Если какое-нибудь ограничение < 0, то необходимо коэффициенты соответствующего ограничения слева и справа до-множить на "-1" и изменить знак неравенства данного ограничения на противоположный. Области, в которых выполняются соответствующие ограничения в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных.

В результате построений получается многоугольник, который определяет пространство решений. Если одно из ограничений имеет знак "=", то ОДР вырождается в отрезок.

В каждой точке, принадлежащей области или границам многоугольника решений, все ограничения выполняются, поэтому все решения, соответствующие этим точкам, являются допустимыми. Пространство решений содержит бесконечное число таких точек, несмотря на это, можно найти оптимальное решение. Для этого необходимо построить в плоскости переменных , градиент целевой функции. Определение оптимальной точки зависит от той задачи, которую необходимо решить.

Если в целевой функции определена задача максимизации, то оптимальная точка будет располагаться в направлении увеличения градиента, если задача минимизации – то в направлении уменьшения градиента целевой функции. Для определения оптимальной точки будем перемещать целевую функцию в направлении увеличения (уменьшения) градиента до тех пор, пока она не сместиться в область недопустимых решений.

После нахождения оптимальной точки пространства решений определяют её координаты ,и значение целевой функции в ней. Правильность выбора оптимальной точки можно проверить расчётом целевой функции в вершинах многогранника решений. В ЗЛП область допустимых решений всегда является выпуклым множеством, т.е. таким множеством, что наряду с любыми двумя точками, принадлежащими этому множеству, этому же множеству принадлежит и отрезок, соединяющий эти две точки. Любая функция наискорейшим образом увеличивается в направлении своего градиента.

Решение задачи линейного программирования симплекс-методом.

Прямая задача.

Рассмотрим задачу линейного программирования в канонической форме:

Найти максимум (минимум) функции 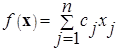при условиях

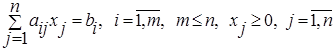
Предполагается, что решение этой задачи существует. Чтобы найти оптимальное решение, надо найти допустимые базисные решения, а из них выбрать оптимальное базисное решение.

Симплекс – метод – это алгебраический метод решения задач линейного программирования. В процессе вычислений производиться последовательный обход вершин многогранника решений (ОДР.) с проверкой в каждой вершине условий оптимальности. При этом каждый переход в смежную вершину сопровождается улучшением целевой функции.

Вычислительные процедуры симплекс - метода.

При графическом методе решения ЗЛП оптимальному решению соответствует всегда одна из угловых (экстремальных) точек пространства решений. Это результат положен в основу построения симплекс-метода. Симплекс-метод не обладает наглядностью геометрического представления пространства решений.

Симплекс-метод реализует упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки, осуществляются последовательные переходы от одной допустимой экстремальной точки к другой, пока не будет найдена точка оптимального решения.

Обозначим: – общее количество переменных в ЗЛП, представленной в канонической форме; - количество исходных переменных; - количество ограничений, - количество дополнительных переменных, тогда .

Каждая вершина многогранника решений имеет - ненулевых переменных и () - нулевых переменных.

Ненулевые переменные называются базисными, нулевые переменные – небазисными.

Дополним систему равенств равенством целевой функции, при этом будем считать, что является базисной переменной, которая всегда присутствует в базисе для любой вершины.

Для получения решения составляется начальный допустимый базис, в котором базисные переменные должны быть представлены в виде единичных орт. Это означает, что уравнения, представляющие данную вершину должны включать каждую базисную переменную только в одной строке с коэффициентом, равным 1.