Реферат: Решение задачи линейного программирования симплекс-методом

Свойство М: При сложении (вычитании) с любой конечной величиной , определяющей любое значение, которое может принимать каждая из переменных исходной ЗЛП, её значение (переменной М) не меняется, а именно,

При составлении начальной симплекс-таблицы все переменные начального допустимого базиса (дополнительные и искусственные) должны располагаться в последних m столбцах перед правой частью.

Алгоритм получения оптимального решения:

1. Переход от неравенств к равенствам с учётом правил перехода - введение остаточных, избыточных, искусственных переменных и коэффициентов штрафа;

2. Определение числа базисных и небазисных переменных;

3. Получение - строки для заполнения СТ(0. Для этого необходимо целевую функцию преобразовать к виду 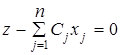; для чего из соответствующих равенств ограничений выразить искусственные переменные и подставить в строку и привести к рациональному виду;

4. Заполнение СТ(0). Перенесение коэффициентов - строки и равенств ограничений в соответствующие строки и столбцы симплекс-таблицы;

5. Исследование функции на условие оптимальности:

определение разрешающего столбца (по знаку и величине коэффициентов небазисных переменных - строки);

определение включаемой переменной из небазисных переменных;

6. Определение разрешающей строки по условию допустимости:

определение минимального отношения при делении правых частей ограничений на положительные коэффициенты разрешающего столбца;

определение исключаемой переменной из начального базиса;

7. Определение разрешающего элемента РЭ;

8. Получение B (0). Замена в матрице начального базиса коэффициентов исключаемой переменной на коэффициенты включаемой переменной; вычисление B (0) по соответствующему правилу;

9. Определение элементов СТ(1) = В(0) СТ(0);

10. Исследование -строки СТ(1) на условие оптимальности.

Если условие не выполнено, то вычисления продолжаются и необходимо повторить пункты 5-10.

Если условие оптимальности выполнено, то решение ЗЛП симплекс-методом закончено, необходимо выделить оптимальные значения переменных и оптимальное значение целевой функции.

Решение задачи линейного программирования симплекс-методом.

Двойственная задача.

Двойственная задача (ДЗ) – это вспомогательная задача линейного программирования, формулируемая с помощью определённых правил непосредственно из условий прямой задачи. Заинтересованность в определении оптимального решения прямой задачи путём решения двойственной к ней задачи обусловлена тем, что вычисления при решении ДЗ могут оказаться менее сложными, чем при ПЗ. Трудоёмкость вычислений при решении ЗЛП в большей степени зависит от числа ограничений, а не от количества переменных. Для перехода к ДЗ необходимо, чтобы прямая задача была записана в стандартной канонической форме. При представлении ПЗ в стандартной форме в состав переменных включаются также избыточные и остаточные переменные.

Двойственная задача имеет:

m переменных, соответствующих числу ограничений прямой задачи;

n ограничений, соответствующих числу переменных прямой задачи.

Двойственная задача получается путём симметричного структурного преобразования условий прямой задачи по следующим правилам:

Каждому ограничению ПЗ соответствует переменная ДЗ;

Каждой переменной ПЗ соответствует ограничение ДЗ;