Реферат: Решение задачи линейного программирования симплекс-методом
4. Формирование симплекс – таблицы на первом шаге:
Начальный базис
СТ (0) РС
 |  |  |  |  |  |  |  | ПЧ | |
| 1 | -1-4M | 3+3M | -3M-3 | M | 0 | 0 | 0 | -12M |
| 0 | 1 | 2 | -2 | 0 | 1 | 0 | 0 | 4 |
| 0 | 3 | -4 | 4 | 0 | 0 | 1 | 0 | 12 |
| 0 | 1 | 1 | -1 | -1 | 0 | 0 | 1 | 0 |
5. Определение разрешающего столбца.
При решении задачи максимизации выбираем в - строке максимально отрицательный коэффициент: 
- включаемая переменная.
6. Определение разрешающей строки: 
– исключаемая переменная.
7. Разрешающий элемент РЭ = 1.
8. Получение матрицы перехода
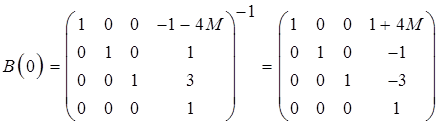, где В(0) - матрица перехода
9. Определение элементов таблицы СТ(1) = В(0) СТ(0);
10. Исследование z-строки СТ(1) на условие оптимальности:
СТ(1)
| z | | | | | | | | ПЧ | |
| z | 1 | 0 | 4+7M | -7M-4 | -3M-1 | 0 | 0 | 1+4M | -12M |
| 0 | 0 | 1 | -1 | 1 | 1 | 0 | -1 | 4 |
| 0 | 0 | -7 | 7 | 3 | 0 | 1 | -3 | 12 |
| 0 | 1 | 1 | -1 | -1 | 0 | 0 | 1 | 0 |
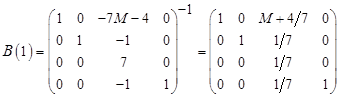
СТ(2)
| z | | | | | | | | ПЧ | |
| z | 1 | 0 | 0 | 0 | 5/7 | 0 | M+4/7 | M-5/7 | 48/7 |
| 0 | 0 | 0 | 0 | 10/7 | 1 | 1/7 | -10/7 | 40/7 |
| 0 | 0 | -1 | 1 | 3/7 | 0 | 1/7 | -3/7 | 12/7 |
| 0 | 1 | 0 | 0 | -4/7 | 0 | 1/7 | 4/7 | 12/7 |
СТ(2) – оптимальная, т. к. коэффициенты при НБП
.
, 
, 
.
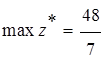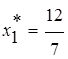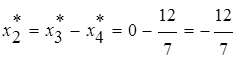3. Решение задачи линейного прог?