Реферат: Серьёзные лекции по высшей экономической математике
7. 10 букв разрезной азбуки: А,А,А,Е,И,К,М,М,Т,Т произвольным образом выкладываются в ряд. Какова вероятность того, что получится слово МАТЕМАТИКА?
Решение. 10 букв можно расположить в ряд числом способов, равным 10! Чтобы получить число благоприятных исходов, нужно взять слово МАТЕМАТИКА и убедиться в том, что его можно получить, переставляя местами 3 буквы А, 2 буквы М и 2 буквы Т, что можно сделать 3!2!2! способами Ответ задачи: 3!2!2!/10!.
8. Брошено 10 игральных костей. Предполагается, что все комбинации выпавших очков равновероятны. Найти вероятность того, что выпала хотя бы одна “6”.
Решение. Общее число исходов здесь равно 610. К благоприятным исходам следует отнести выпадение одной, двух, трёх и т. д. шестёрок. Проще подсчитать число неблагоприятных исходов, то есть исходов, когда не выпало ни одной шестёрки. Их, очевидно, 510, и число благоприятных исходов равно 610 – 510. Искомая вероятность равна 1 – ![]() .
.
9. В мешке находятся 10 различных пар обуви. Из мешка наугад извлекаются 6 единиц обуви. Найти вероятность того, что в выборку не попадёт двух единиц обуви, составляющих одну пару.
Решение. Общее число исходов – это количество возможных выборок объёмом в 6 единиц из общего числа в 20 единиц, то есть ![]() – число сочетаний из двадцати по шесть. Подсчитаем число благоприятных исходов. Очевидно, что все возможные выборки, удовлетворяющие условию задачи, можно составить следующим образом: выбрать 6 пар обуви, что осуществляется числом способов, равным
– число сочетаний из двадцати по шесть. Подсчитаем число благоприятных исходов. Очевидно, что все возможные выборки, удовлетворяющие условию задачи, можно составить следующим образом: выбрать 6 пар обуви, что осуществляется числом способов, равным ![]() , затем из каждой пары выбрать одну единицу. Из одной пары это можно сделать двумя способами, из двух – четырьмя, из трёх – восемью и т. д. Таким образом можно перебрать все
, затем из каждой пары выбрать одну единицу. Из одной пары это можно сделать двумя способами, из двух – четырьмя, из трёх – восемью и т. д. Таким образом можно перебрать все ![]() шестёрок, удовлетворяющих условию задачи. Искомая вероятность равна
шестёрок, удовлетворяющих условию задачи. Искомая вероятность равна 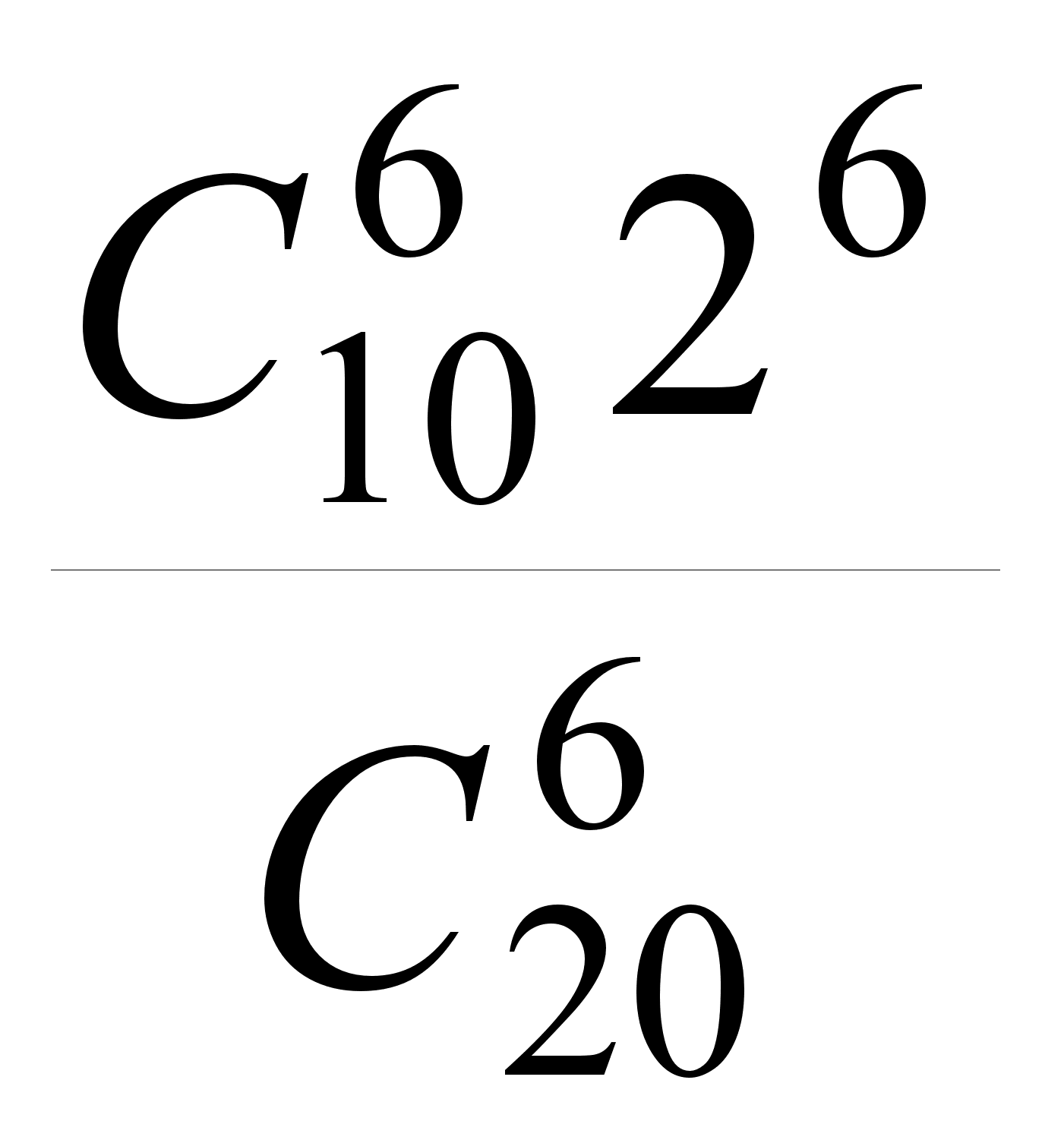 .
.
1.а. В условиях задачи 1. подсчитать вероятность того, что при раздаче карт по одной по кругу четырём игрокам каждому достанется один туз. (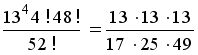 0,1055,
0,1055, 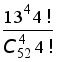 )
)
1.б. В условиях предыдущей задачи подсчитать вероятность того, что все тузы достанутся одному игроку.
1.в. n лиц рассаживаются в ряд в случайном порядке. Какова вероятность, что два определенных лица окажутся рядом? Найти соответствующую вероятность , если те же лица садятся за круглый стол.
2.а. Решите задачу 2. при условии, что каждая партия кончается либо выигрышем одного из участников, либо ничьей, и всевозможные исходы партий равновероятны.
2.б. В лифт 8-этажного дома на первом этаже вошли 5 человек. Предположим, что каждый из них с равной вероятностью может выйти на любом из этажей, начиная со второго. Найти вероятность того, что все пятеро выйдут на разных этажах.
3.а. Брошены шесть игральных костей. Найти вероятность следующих событий:
а) на всех костях выпало разное количество очков;
б) суммарное количество выпавших очков равно 7.
3.б. Найти вероятность того, что среди произвольно выбранных 12-ти человек все имеют дни рождения в разные месяцы.
4.а. В условиях задачи 4. найти вероятность того, что шары разноцветные.
5.а. В кармане лежат 10 ключей, из которых к данному замку подходит лишь один, но неизвестно, какой. Из кармана извлекаются ключи случайным образом один за другим и делается попытка открыть замок. Найти вероятность того, что замок будет открыт с 7-й попытки.
5.б. Студент Иванов при подготовке к экзамену из 30-и билетов выучил лишь 20. Группа сдающих экзамен студентов состоит из 16-и человек, причём каждый по очереди берёт один билет, не возвращая его. В каком случае студент Иванов с большей вероятностью сдаст экзамен: если он будет в этой очереди первым или если он будет последним?
5.в. Партия из 25-и приборов содержит один неисправный прибор. Из этой партии для контроля выбраны случайным образом 6 приборов. Найти вероятность того, что неисправный прибор попал в выборку.
5.г. Ящик содержит 90 годных и 10 дефектных шурупов. Если использовать 10 шурупов, какова вероятность того, что ни один из них не окажется дефектным? Какова вероятность того, что среди них окажется 4 дефектных шурупа?
6.а. В n ящиках размещают n шаров так, что для каждого шара равновозможно попадание в любой ящик. Найти вероятность того, что ни один ящик не пуст.
6.б. Каждая из n палок разламывается на две части – длинную и короткую. Затем 2n обломков объединяются в n пар, каждая из которых образует новую “палку”. Найти вероятность того, что а)части будут соединены в первоначальном порядке; б) все длинные части будут соединены с короткими.
6.в.Для уменьшения общего количества игр 2n команд спортсменов разбиваются на две подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся: а) в разных подгруппах, б) в одной подгруппе. Ответ: а) n/(2n-1); б) (n–1)/(2n-1);
7.а. Из букв разрезной азбуки составлено слово СТАТИСТИКА. Затем из этих букв случайным образом без возвращения отобрано 5 букв. Найти вероятность того, что из отобранных букв можно составить слово ТАКСИ. Ответ 2/21.
8.а. Чему равна вероятность того, что два бросания трёх игральных костей дадут один и тот же результат, если а) кости различимы, б) кости неразличимы. Ответ: 1/216; 83/3888.
8.б. Из 28 костей домино случайным образом выбираются две. Найти вероятность того, что из них можно составить “цепочку” согласно правилам игры. Ответ: 7/18.
8.в. Брошено 10 игральных костей. Найти вероятность событий: а) выпало ровно 3 шестёрки, б) выпало хотя бы две шестёрки.
9.а. Два игрока независимым образом подбрасывают (каждый свою) монеты. Найти вероятность того, что после n подбрасываний у них будет одно и то же число гербов. Ответ: ![]() .
.
Решение задачи 1.а.