Реферат: Шарнирно-рычажные, фрикционные и зубчатые механизмы: общие сведения и расчеты

Фрикционные механизмы применяются в приводах систем, в устройствах транспортирования различных носителей информации. Передача движения в них осуществляется за счет сил трения между звеньями.

3. Зубчатые механизмы

3.1. Общие сведения

Зубчатые механизмы чаще по сравнению с другими видами механизмов применяются в машиностроении, приборостроении, в технических системах. Они служат для преобразования вращательного движения ведущего звена и передачи моментов сил.

Достоинствами таких передач являются постоянство заданного передаточного отношения, компактность, высокий КПД (0,92 … 0,98); наличие небольших сил давления на валы и опоры; высокая надежность; простота обслуживания. К недостаткам можно отнести сложность и высокую точность изготовления и сборки, наличие шума при работе, невозможность плавного бесступенчатого регулирования скорости вращения ведомого звена.

Все понятия, параметры и их обозначения, относящиеся к геометрии и кинематике зубчатых передач, стандартизированы.

Меньшее из пары зубчатых колес принято называть шестерней, большее – колесом. Термин «зубчатое колесо» можно применять как к шестерне, так и к колесу зубчатой передачи. Индексы «1» и «2» присваивают соответственно параметрам шестерни и колеса.

Зацепление зубчатых колес можно кинематически представить как качение без скольжения друг по другу двух поверхностей, называемых начальными. Для цилиндрических передач это цилиндры, для конических – конусы. Точку качения начальных поверхностей определяют как полюс зацепления.

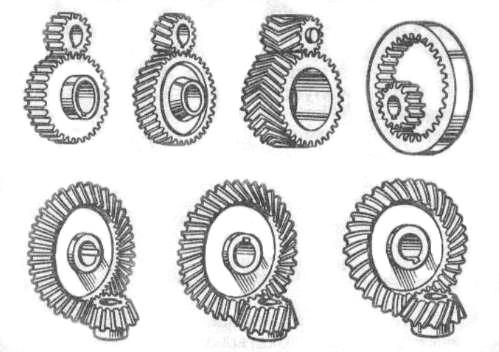
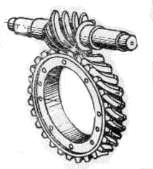
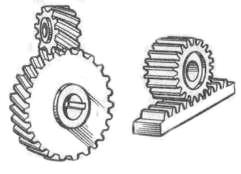
По числу пар зацепляющихся колес зубчатые передачи бывают одно-, двух- и многоступенчатыми. По взаимному расположению осей их делят на цилиндрические – с параллельными осями (рис. 5, а), конические – с пересекающимися осями (рис. 5, д), на червячные (рис. 3.5, з), винтовые (рис. 5, и) – со скрещивающимися в пространстве осями. По расположению зубьев относительно образующих начальной поверхности колеса зубчатые передачи делят на прямозубые (рис. 5, а) и косозубые (рис. 5, б, в), шевронные (рис. 5, в) и с круговым зубом (рис. 5, ж).

Прямозубыми называются колеса (передачи), направление каждого зуба которых совпадает с образующей начальной поверхности (цилиндра или конуса). Косозубыми называются зубчатые колеса, направление каждого зуба которых составляет некоторый постоянный угол с образующей начальной поверхности. Шевронными называются колеса (рис. 5, в), зубчатый венец которых образуется из двух рядов косых зубьев противоположного направления.

Конические колеса могут быть прямозубыми, косозубыми и с круговым зубом

(рис.5, д, е, ж).

Зацепление зубчатых колес может быть внешним и внутренним

(рис.5, г).

Реечные зубчатые передачи (рис. 5, к) преобразуют вращательное движение в поступательное или наоборот.

г

в

а

б

д е ж

к

з и

Рис. 5

Наибольшее распространение получили передачи с эвольвентным профилем зубьев. Во-первых, эвольвентное зацепление мало чувствительно к отклонениям межосевого расстояния, не нарушается правильность зацепления. Во-вторых, профиль зубьев инструмента для нарезания эвольвентных зубчатых колес может быть прямолинейным, сравнительно простое изготовление и контроль инструмента и колес, одним инструментом можно нарезать колеса с разным числом зубьев. Траекторией точки контакта эвольвентных профилей зубьев является прямая линия.

По конструктивному выполнению корпуса зубчатые передачи бывают открытыми и закрытыми. Открытые не имеют защиты от попадания пыли и грязи, закрытые передачи имеют жесткий корпус и работают в масляной ванне.

По характеру своей работы передачи могут быть реверсивные и нереверсивные. Реверсивные передачи характеризуются поочередным изменением на противоположное направления движения ведущего звена.

По величине окружной скорости различают передачи – тихоходные (до 3 м/с), средних скоростей (3 … 15 м/с) и быстроходные (свыше 15 м/с).

Отношение угловых скоростей ведущего и ведомого колес называют передаточным отношением i, а отношение числа зубьев колеса к числу зубьев шестерни – передаточным числом u. Для редукторов (замедляющих передач) абсолютные значения i и u совпадают. Передаточное число относится только к паре зубчатых колёс, оно всегда положительное, больше единицы и является частным случаем передаточного отношения. Число зубьев колес обозначают буквой z с индексом, соответствующим индексу колеса. Основной характеристикой размеров зубьев является модуль m – отношение окружного шага к числу π. Модули стандартизированы и имеют размерность в миллиметрах. Зубчатые колеса (передачи) с модулем m < 1 называют мелкомодульными.

3.2. Параметры цилиндрических прямозубых колес

Рассмотрим элементы зубчатых колес (рис. 6), находящихся в зацеплении, в плоскости, перпендикулярной к оси вращения. По высоте снаружи зубья ограничены окружностью выступов диаметром da, изнутри – окружностью впадин диаметром df. Боковые поверхности полного профиля зуба очерчены эвольвентами противоположных ветвей. Эвольвента представляет собой траекторию произвольной точки прямой, перекатывающейся без скольжения по окружности, называемой основной. Положительная ветвь эвольвенты получается при перекатывании производящей прямой против хода часовой стрелки, отрицательная – по ходу часовой стрелки. С увеличением радиуса основной окружности до бесконечности (зубчатая рейка) эвольвента превратится в прямую. Часть бокового профиля зуба очерчивается по переходной кривой, служащей плавным переходом от эвольвенты к окружности впадин. Наличие переходной кривой делает зуб более прочным у основания. При зацеплении одного колеса с другим появляется начальная окружность радиусом rw. Это окружность одного зубчатого колеса, перекатывающаяся без скольжения по окружности (поверхности) второго из зацепляющихся колес. Расстояние между одноименными профилями соседних зубьев по дуге окружности называется окружным шагом и обозначается p_t . Значение этого параметра по начальным окружностям должно быть одинаковым у находящихся в зацеплении колес. Пользуясь шагом зацепления, можно выразить длину любой окружности колеса, умножив шаг на число зубьев z:

ptz = πd_t , (17)

где _t – индекс соответствующей окружности, например, p_a , d_a или p_f , d_f .

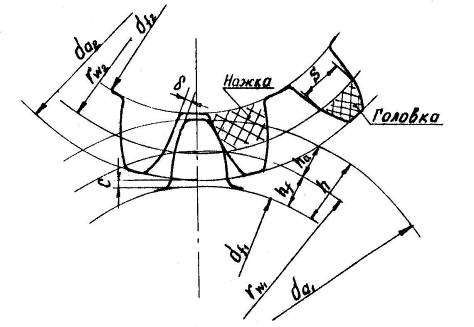
Рис. 6

Величина pt выражается несоизмеримым числом, так как в правую часть условия (17) входит число π. Это затрудняет выбор размеров колес при их проектировании и изготовлении. Поэтому основным параметром принят не шаг, а отношение его к числу π. Эта величина называется модулем зацепления mt:

m_t = p_t /π. |мм| (18)

Шаг и модуль имеют индекс той окружности, по которой они измерены. Величины модулей для снижения номенклатуры и унификации режущего и контролирующего инструмента стандартизированы. Чаще всего согласно стандартам ограничиваются следующими значениями модуля (в миллиметрах): 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,20; 0,25; 0,3; 0,5; 0,6; 0,8; 1,0; 1,25; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0. Окружность, по которой модуль имеет расчетное стандартное значение, называется делительной. Диаметр ее обозначается d, она является базовой для определения элементов зубьев и их размеров. Шаг и модуль по делительной окружности обозначают соответственно р и m.

Диаметр делительной окружности

d = mz. (19)

Для наиболее распространенных неисправленных по высоте (нулевых) колес начальная и делительные окружности совпадают и передаточное отношение для пары таких колес будет равно