Реферат: Симлекс-метод
4. Делают один шаг (итерацию) метода полного исключения Гаусса с направляющим элементом aij, для чего используют соотношения (3.3.16) - (3.3.18). В частности, элементы индексной строки новой таблицы вычисляют в соответствии с формулой
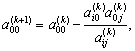
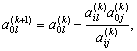l=1,2, ..., n.
Правильность вычислений контролируют по формулам непосредственного счета:
(3.3.23)
(3.3.24)
В столбце Bx новой таблицы заменяют xi на xj, а в столбце С ci на cj.
5. Если все a0l(k+1)³0, l=1,.,n, то новое базисное решение xi= ai0(k+1), iÎIб(k+1) - оптимально. В противном случае переходят к этапу 2 и выполняют очередную итерацию.
6. Второй, третий и четвертый этапы повторяют до тех пор, пока одна из итераций не закончится одним из двух исходов:
а) все a0l ³0. Это признак (критерий) оптимальности базисного решения последней симплекс-таблицы;
б) найдется такой a0j=Dj<0, что все элементы этого столбца arj£0,
r = 1, ., m. Это признак неограниченности целевой функции z=
cjxj на множестве допустимых решений задачи.
Назовем некоторые особенности применения табличного симплекс-метода.
Если в качестве начального базиса выбирают базис из свободных переменных, для которых ci=0, то оценки для всех небазисных переменных равны Dj = a0j = -cj, а соответствующее значение целевой функции
a00=
cixi=0, iÎIб.
Отсутствие векторов с отрицательными оценками при решении задач максимизации является признаком оптимальности соответствующего базисного решения.
Если существует такой небазисный вектор, для которого оценка отрицательна, а все элементы этого столбца неположительны, то целевая функция задачи в области допустимых решений неограничена.
При решении задач минимизации в базис вводится вектор с наибольшей положительной оценкой, а отсутствие таких векторов является признаком оптимальности последнего базисного решения.
Пример 3.4.
Максимизировать 4x1+3x2
при ограничениях
x1 £ 4000;
x2 £ 6000;
x1 + 
x2 £ 6000;
x1, x2 ³ 0.
Расширенная форма задачи имеет такой вид:
максимизировать 4x1+3x2
при ограничениях
1x1 + 0x2 + 1x3 + 0x4 + 0x5 = 4000;
0x1 + 1x2 + 0x3 + 1x4 + 0x5 = 6000;