Пусть даны действительная m ´n –матрица A ранга k £min(m,n) и действительный m –вектор b . Найти действительный n –вектор x ₀ , минимизирующий евклидову длину вектора невязки Ax–b .

Пусть y – n – мерный вектор фактических значений, x – n – мерный вектор значений независимой переменной, b – коэффициенты в аппроксимации y линейной комбинацией n заданных базисных функций j :

.

Задача состоит в том, чтобы в уравнении подобрать такие b , чтобы минимизировать суммы квадратов отклонений e=y–Xb , где X – есть так называемая матрица плана, в которой строками являются n – мерный вектора с компонентами, зависящими от x_j : каждая строка соответствует определенному значению x_j . Коэффициенты можно найти решая нормальные уравнения , откуда . Покажем это. Возведем в квадрат выражение для е :

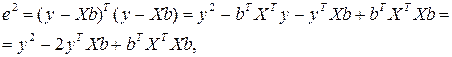
т. к. .

Это выражение имеет экстремум в точке, где 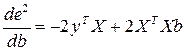=0

Откуда и получаем .

Следует отметить, что последнее выражение имеет в определенной степени формальный характер, т. к. решение нормальных уравнений, как правило, проводится без вычисления обратной матрицы (метод Крамера) такими методами как метод Гаусса, Холесского и т. д.

Пример. Пусть заданы результаты четырех измерений (рис. 1): y= 0 при x= 0; y= 1 при x= 1; y= 2 при x= 3; y= 5 при x= 4. Задача заключается в том, чтобы провести через эти точки прямую таким образом, чтобы сумма квадратов отклонений была минимальна. Запишем уравнение, описывающее проведение прямой по результатам измерений. Мы получаем переопределенную систему:

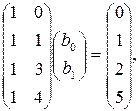
или Xb=y . Нам понадобится матрица X^T X и обратная к ней:

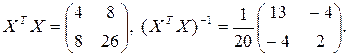
Тогда решение b=(X^T X )^-1 X^T y по методу наименьших квадратов будет иметь вид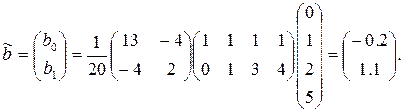

Таким образом, оптимальная прямая задается уравнением Метод точечной квадратичной аппроксимации (метод наименьших квадратов) не предполагает, что мы должны приближать экспериментальные данные лишь с помощью прямых линий. Во многих экспериментах связи могут быть нелинейными, и было бы глупо искать для этих задач линейные соотношения. Пусть, например, мы работаем с радиоактивным материалом. Тогда выходными данными у являются показания счетчика Гейгера в различные моменты времени t . Пусть наш материал представляет собой смесь двух радиоактивных веществ, и мы знаем период полураспада каждого из них, но не знаем, в каких пропорциях эти вещества смешаны. Если обозначить их количества через С и D , то показания счетчика будут вести себя подобно сумме двух экспонент, а не как прямая:

. (1)

На практике, поскольку радиоактивность измеряется дискретно и через различные промежутки времени, показания счетчика не будут точно

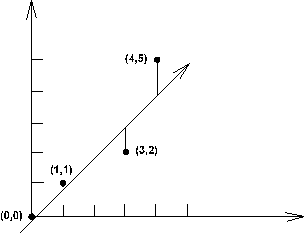
Рис. 1. Аппроксимация прямой линией.

соответствовать (1). Вместо этого мы имеем серию показаний счетчика в различные моменты времени , и (1) выполняется лишь приближенно:

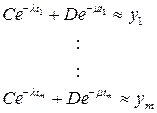
Если мы имеем более двух показаний, m> 2, то точно разрешить эту систему относительно C и D практически невозможно. Но мы в состоянии получить приближенное решение в смысле минимальных квадратов.

Ситуация будет совершенно иной, если нам известны количества веществ C и D и нужно отыскать коэффициенты l и m. Это нелинейная задача наименьших квадратов, и решить ее существенно труднее. Мы по–прежнему будем минимизировать сумму квадратов ошибок, но сейчас она уже не будет многочленом второй степени относительно l и m, так что приравнивание нулю производной не будет давать линейных уравнений для отыскания оптимальных решений.

Глава 1. Метод наименьших квадратов

1.1. Задача наименьших квадратов

Задача наименьших квадратов заключается в минимизация евклидовой длины вектора невязок || Ax-b ||.

Теорема 1. Пусть А – m ´n – матрица ранга k , представленная в виде

A= HRK^T (2)

где H ортогональная m ´m матрица; R – m ´n – матрица вида

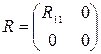, (3)

где: R ₁₁ – k xk – матрица ранга k ; K – ортогональная k xk – матрица. Определим вектор

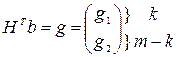(4)

и введем новую переменную

. (5)

Определим как единственное решение системы R ₁₁ y ₁ =g ₁ . Тогда:

1. Все решения задачи о минимизации ||Ax-b || имеют вид 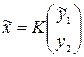, где y ₂ произвольно.

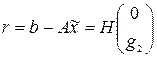2. Любой такой вектор приводит к одному и тому же вектору невязки . (6)