Реферат: СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ В ЛИНЕЙНОЙ ЗАДАЧЕ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ

4. Единственным решением минимальной длины является вектор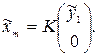

Доказательство . В выражении для квадрата нормы невязки заменим A на HRK^T в соответствии с (2) и умножая на ортогональную матрицу H^T (умножение на ортогональную матрицу не меняет евклидову норму вектора) получим

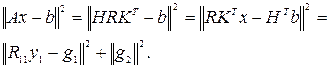(7)

Далее из (3) и (5) следует, что

.

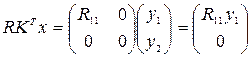Из (4) следует

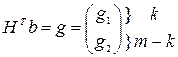
Подставляя оба последних выражения в (7) получим

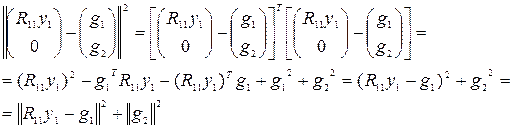
Последнее выражение имеет минимальное значение при R ₁₁ y ₁ =g ₁ , а в этом уравнении единственным решением является , так как ранг матрицы R ₁₁ равен к . Общее решение y выражается формулой 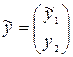, где y ₂ произвольно. Для вектора имеем

,

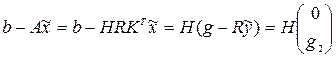что устанавливает равенство (3). Среди векторов наименьшую длину имеет тот, для которого y ₂ =0. Отсюда следует, что решением наименьшей длины будет вектор . Теорема доказана.

Всякое разложение матрицы А типа (2) мы будем называть ортогональным разложением А . Заметим, что решение минимальной длины, множество всех решений и минимальное значение для задачи минимизации ||Ax-b || определяются единственным образом. Они не зависят от конкретного ортогонального разложения.

При проведении разложения необходимо приводить матрицы к диагональному виду. Для этого обычно используются два преобразования: Гивенса и Хаусхолдера, оставляющие нормы столбцов и строк матриц неизменными.

1.2. Ортогональное вращение Гивенса

Лемма. Пусть дан 2–вектор , причем либо .Существует ортогональная 2´2 матрица такая, что:

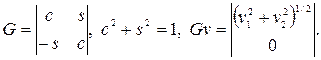(8)

Доказательство. Положим:

.

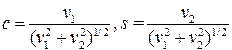Далее прямая проверка.

Матрица преобразования представляет собой матрицу вращений

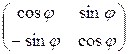
или отражений

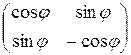
1.3. Ортогональное преобразование Хаусхолдера

Применяется для преобразования матриц к диагональному виду. Матрица преобразования представляет из себя следующее выражение: 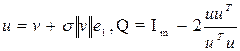, (9)

или, если вектор v нормирован, т.е. используется вектор единичной длины , то . В обоих случаях H – симметричная и ортогональная матрица. Покажем это:

.

Отсюда следует: что , т.е. симметричность и ортогональность. В комплексном случае матрица эрмитова[1] и унитарна[2] . Предположим, что дан вектор х размерности m , тогда существует матрица H такая, что , где

а s = + 1, при положительной первой компоненте вектора х и = –1, при отрицательной.

Доказательство. Положим действительная матрица. Любую действительную матрицу можно привести в треугольному виду

Далее принимаем во внимание то, что и получаем следующее:

1.4. Сингулярное разложение матриц

Пусть X – матрица данных порядка N xp , где N>p , и пусть r – ранг матрицы X . Чаще всего r=p , но приводимый ниже результат охватывает общий случай, он справедлив и при условии r<p .

Теорема о сингулярном разложении утверждает, что

(10)

где V – матрица порядка N xr , столбцы которой ортонормированы, т.е. ; U – матрица с ортонормированными столбцами порядка p xr ; таким образом, ; Г – диагональная матрица порядка r xr , диагональные элементы которой , называемые сингулярными числами матрицы X , положительны. Используя диагональные элементы матрицы Г, столбцы матрицы V , и столбцы матрицы U , сингулярное разложение матрицы X , определяемое по (10), можно записать в виде:

(11)

Имеют место следующие фундаментальные соотношения.

· Квадратная симметричная матрица XX' порядка N xN , имеет r положительных и N–r нулевых собственных чисел. Положительными собственными числами XX' являются , а соответствующими собственными значениями – . Таким образом, сингулярные значения – это положительные квадратные корни из положительных собственных чисел матрицы XX' , а столбцы матрицы V – соответствующие собственные векторы.

· Квадратная симметричная матрица X'X порядка p xp , имеет r положительных и p–r нулевых собственных чисел. Положительными собственными числами X'X являются , а соответствующими собственными значениями – , таким образом, сингулярные значения – это положительные квадратные корни из положительных собственных чисел матрицы X'X , а столбцы матрицы U – соответствующие собственные векторы.

Положительные собственные числа матрицы X'X и XX' совпадают и равны . Более того, если u_m – собственный вектор матрицы X'X , а v_m – собственный вектор матрицы XX' , соответствующие одному и тому же собственному числу , то u_m и v_m связаны следующим соотношением

(12)

Эти соотношения дают возможность вычислять , зная , и наоборот. В компактной форме эти соотношения можно записать следующим образом:

. (13)

Исследование матрицы X'X в факторном анализе называется R- модификацией, а XX' – Q– модификацией. Соотношения (12)–(13) показывают, что результаты Q– модификации можно получить по результатам R– модификации и наоборот.