Нормой вектора x в пространстве векторов называется функционал, обозначаемый , удовлетворяющий следующим условиям:

1) положительной определенности –

2) положительной однородности – ;

3) неравенству треугольника – .

Нормой квадратной матрицы А в пространстве матриц, согласованной с нормой вектора называется функционал 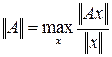, удовлетворяющий условиям 1 – 3 для нормы вектора:

1) ;

2)

3)

4) мультипликативное неравенство –

Наиболее употребимы следующие нормы для векторов:

· норма суммы модулей

· евклидова норма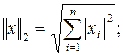

· норма максимума модуля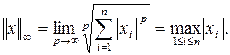

Нормы матриц:

·

·

·

Здесь являются сингулярными числами[3] матрицы А ; это положительные значения квадратных корней из собственных значений матрицы А^Т А (которая при невырожденной матрице А положительно определена[4] , в противном случае положительно полуопределена (неотрицательно определена[5] ) и поэтому имеет только вещественные собственные значения ³ 0). Для вещественных симметричных матриц сингулярные числа равны абсолютным величинам собственных значений: .

Умножение вектора х на матрицу А приводит к новому вектору Ах , норма которого может очень сильно отличаться от нормы вектора х .

Область изменений может быть задана двумя числами

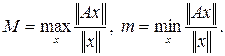
Максимум и минимум берутся по всем ненулевым векторам. Заметим, что если А вырождена, то m= 0. Отношение M/m называется числом обусловленности матрицы А ,

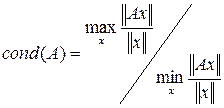(7)

Рассмотрим норму обратной[6] матрицы .

Для матрицы А существует сингулярное разложение , тогда , отсюда . Аналогично для обратной матрицы и . Отсюда следует, что собственные числа матрицы – 1/ есть величины, обратные собственным числам матрицы – . При этом очевидно, что 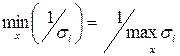. Из последнего выражения вместе с (7) следует . Таким образом обусловленность матрицы равна произведению нормы матрицы на норму обратной матрицы.

Рассмотрим систему уравнений Ax=b , и другую систему, полученную изменением правой части: A(x+ Dx)=b+ Db . Будем считать Db ошибкой в b , а Dx соответствующей ошибкой в x , хотя нам нет необходимости считать ошибки малыми. Поскольку A( Dx)= Db , то определения M и m немедленно приводят к неравенствам Следовательно , при m ¹ 0,

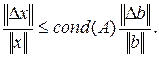
Величина есть относительное изменение правой части, а величина – относительная ошибка, вызванная этим изменением. Аналогичные выкладки можно провести не только с элементами вектора правой части но и с элементами самой матрицы А и найти зависимость между относительным изменением элементов матрицы и относительной ошибкой вызванной этим изменением. Отсюда следует, что число обусловленности выполняет роль множителя в увеличении относительной ошибки.

Приведем некоторые свойства числа обусловленности. Ясно, что M ³m и поэтому cond(А) ³ 1. Если Р – матрица перестановок[7] , то компоненты вектора Px лишь порядком отличаются от компонент вектора х . Отсюда следует, что и cond(P)= 1 . В частности cond(I)= 1. Если А умножается на скаляр с , то cond(cА)= cond(А) . Если D – диагональная матрица, то

глава 2. Реализация сингулярного разложения

2.1. Алгоритмы

QR –алгоритм начинается с разложения матрицы по Грамму-Шмидту , затем меняются местами сомножители: Эта матрица подобна первоначальной, Этот процесс продолжается, причем собственные значения не изменяются:

Эта формула описывает QR –алгоритм без сдвигов. Обычно время которое тратится на такой процесс пропорционально кубу размерности матрицы – n ³ . Необходимо процесс ускорить, для чего используется предварительное приведение матрицы А к форме Хессенберга[8] а также используется алгоритм со сдвигом. Форма Хессенберга представляет из себя ?