Реферат: СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ В ЛИНЕЙНОЙ ЗАДАЧЕ МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ

Теорема 4 . Пусть А – m ´n– матрица ранга к . Найдутся ортогональная m ´m– матрица Н и ортогональная n ´n– матрица К такие, что

(19)

причем R ₁₁ – невырожденная треугольная к ´к– матрица.

Заметим, что выбором Н и К в уравнении (19) можно добиться, чтобы R ₁₁ была верхней или нижней треугольной.

В (19) матрица А представлена произведением A= HRK ^T , где R – некоторая прямоугольная матрица, ненулевые компоненты которой сосредоточены в невырожденной треугольной подматрице. Далее мы покажем, что эту невырожденную подматрицу R можно упростить далее до невырожденной диагональной матрицы. Это разложение тесно связано со спектральным разложением симметричных неотрицательно определенных матриц A ^T A и AA ^T (см. 11).

Теорема 5. Пусть А – m ´n– матрица ранга k . Тогда существуют ортогональная m ´m– матрица U , ортогональная n ´n– матрица V и диагональная m ´n– матрица S такие, что

U ^T AV= S , A= USV ^T (20)

Матрицу S можно выбрать так, чтобы ее диагональные элементы составляли невозрастающую последовательность; все эти элементы неотрицательны и ровно к из них строго положительны.

Диагональные элементы S называются сингулярными числами А . Докажем сперва лемму для специального случая m=n=rankA .

Лемма 2. Пусть А – n ´n –матрица ранга n . Тогда существует ортогональная n ´n –матрица U , ортогональная n ´n –матрица V и диагональная n ´n –матрица S такие, что U ^T AV= S , A= USV ^T и последовательные диагональные элементы S положительны и не возрастают.

Доказательство леммы . Положительно определенная симметричная матрица A ^T A допускает спектральное разложение

A ^T A =VDV ^T , (21)

где V – ортогональная n ´n –матрица, а D – диагональная матрица, причем диагональные элементы D положительны и не возрастают. Определим S как диагональную n ´n –матрицу, диагональные элементы которой суть положительные квадратные корни из соответствующих диагональных элементов D . Таким образом

D= S ^T S= S ² , S ^-1 D ^S-1 =I . (22)

Определим матрицу

U= AVS ^-1 (23)

Из (21), (22), (23) и ортогональности V следует, что

U ^T U=S ^-1 V ^T A ^T AVS ^-1 =S ^-1 DS ^-1 =I т.е. U ортогональна. Из (23) и ортогональности V выводим USV ^T =AVS ^-1 SV ^T =AVV ^T =A Лемма доказана.

Доказательство теоремы 5 . Пусть A= HRK ^T , где H, R, K ^T имеют свойства, указанные в теореме 4. Так как R₁₁ из (19) – невырожденная треугольная к ´к– матрица, то согласно лемме 2 , можно написать

(24)

Здесь и – ортогональные к ´к– матрицы, а – невырожденная диагональная матрица, диагональные элементы которой положительны и не возрастают. Из (24) следует, что матрицу R в уравнении (19) можно записать в виде

(25)

где:

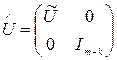– ортогональная m ´m– матрица;

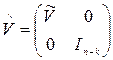– ортогональная n ´n– матрица;

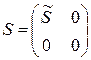– ортогональная m ´n– матрица;

Теперь, определяя U и V формулами

(26)

заключаем из (24) – (26), что A= USV ^T , где U, S, V имеют свойства, указанные в формулировке теоремы 5. Это завершает доказательство.

Заметим, что сингулярные числа матрицы А определены однозначно, в то время, как в выборе ортогональных матриц U, V есть произвол. Пусть s – сингулярное число А , имеющее кратность l . Это значит, что для упорядоченных сингулярных чисел найдется индекс I такой, что

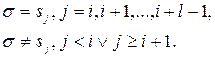
Положим k=min(m,n ), и пусть Q – ортогональная к ´к– матрица вида

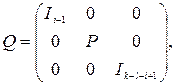
Здесь Р – ортогональная l ´l– матрица Если A= USV ^T – сингулярное разложение А и s _i =…=s _{i+ l -1} , то сингулярным разложением А будет также и , где .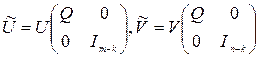

1.6. Число обусловленности

Некоторые вычислительные задачи поразительно чувствительны к изменению данных. Этот аспект численного анализа не зависит от плавающей арифметики или выбранного алгоритма.

Например:

Найти корни полинома: (x -2)² =10^-6

Корни этого уравнения есть 2+10^-3 и 2-10^-3 . Однако изменение свободного члена на 10^-6 может вызвать изменение в корнях, равное 10^-3 .

Операции с матрицами, как правило, приводят к решению систем линейных уравнений. Коэффициенты матрицы в правой части системы линейных уравнений редко известны точно. Некоторые системы возникают из эксперимента, и тогда коэффициенты подвержены ошибкам наблюдения. Коэффициенты других систем записываются формулами, что влечет за собой ошибки округлений. В связи с этим необходимо знать, как влияют ошибки в коэффициентах матрицы на решение. Именно для этого вводится понятие обусловленности матрицы.