Реферат: Синтез комбинацонных схем и конечных автоматов, сети Петри

д) разработать логическую схему автомата в базисе И – НЕ, реализуя элементы памяти на триггерах и задержках.

2.2 Теоретические сведения

Конечным автоматом называется такое дискретное устройство, выходные сигналы которого в определённые моменты времени зависят не только от последнего пришедшего входного сигнала, но и от некоторого количества предыдущих его значений.

Различают синхронные и асинхронные автоматы. У асинхронных смена выходных сигналов y(tj) может происходить только в моменты изменения входных x(tj) , у синхронных – в моменты времени, определяемые дополнительным синхронизирующим сигналом c(t) .

Определим множества, которым могут принадлежать входные и выходные сигналы (условимся обозначать tj как j):

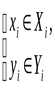– множетва входных и выходных сигналов.

Тогда выражения

(2.2.1)

определяют входной и выходной алфавиты автомата.

Пусть . Тогда если y(j) = λ(x(j)), то этот автомат является, очевидно, комбинационной схемой.

Введём дополнительную переменную для того, чтобы охарактеризовать состояние автомата в каждый момент времени j:

(2.2.2)

В том случае, если X, Y и S – конечные множества, то и сам автомат называют конечным.

В виде уравнений любой конечный автомат можно записать разными способами. Одна из возможных форм записи:

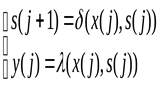(2.2.3)

Записанный таким образом автомат называется автоматом Мили. Ясно, что это – более информативная форма записи по сравнению с автоматом Мура:

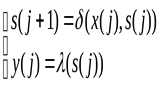(2.2.4)

Способы задания автоматов.

Во - первых, автомат может быть задан непосредственно уравнениями вида (2.2.3) или (2.2.4).

Во - вторых, уравнения (2.2.3) и (2.2.4) могут быть представлены в табличной форме. Табличный аналог первого уравнения в (2.2.3) называется таблицей переходов, второго – таблицей выходов.

В - третьих, таблицы переходов и выходов можно объединить в одну. Содержимое каждой клетки представляет собой дробь: над косой чертой вписывается соответствующее значение из таблицы переходов, под косой чертой – значение из таблицы выходов. Полученная таким образом таблица называется общей таблицей переходов и выходов конечного автомата.

Граф автомата – это сигнальный граф, вершины которого обозначают состояния автомата, на дугах отражены условия перехода из состояния в состояние и значения выходных сигналов в виде дроби: над косой чертой – x(j), под ней – y(j).

Конечный автомат можно также описать с помощью матрицы переходов. Это аналог графа в табличной форме. Она представляет собой квадратную матрицу размерности число состояний число состояний, в которой отражены условия перехода из состояния в состояние аналогично изображённым на графе.

Общее определение конечного автомата:

M = (X, Y, S, δ, λ), (2.2.5)

где X – входной алфавит, Y – выходной алфавит, S – множество состояний, δ – функция переходов, λ – функция выходов.

Пусть имеется два автомата: M и M’.

Если для любого существует по крайней мере одно , эквивалентное ему, то говорят, что M’ покрывает M: M’ ≥ M.

Если одновременно M’ ≥ M и M ≥ M’, то M ~ M’ . Получаем эквивалентные автоматы. В этом случае невозможно различить M и M’ по их реакции на входные сигналы.