Реферат: Система управления аппаратом производства фотографической эмульсии

Проведя вычисления по формулам (2.14) и (2.15), найдем начальное условие для площади теплообмена F₀ = 1.381 м² .

Чтобы вычислить площадь теплообмена как функцию времени, воспользуемся следующими соображениями. За некоторое малое время Δt при подаче реагентов в реактор уровень в нем повысится на некоторую малую величину Δh . При этом площадь теплообмена и объем тоже получат приращения:

; .

Выразив из второго выражения Δh и подставив его в первое, получим:

.

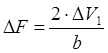Устремляя Δt к нулю и интегрируя, получим:

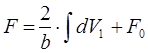. (2.16)

Величина dV₁ легко выражается из (2.9).

Для нахождения коэффициента теплопередачи воспользуемся формулой:

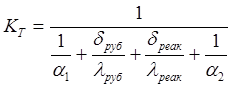, (2.17)

в которой приняты следующие обозначения:

α₁ – коэффициент теплоотдачи от воды в рубашке к стенке рубашки;

δ_руб – толщина стенки рубашки;

λ_руб – коэффициент теплопроводности стенки рубашки;

δ_реак – толщина стенки реактора;

λ_реак – коэффициент теплопроводности стенки реактора;

α₂ – коэффициент теплоотдачи от стенки реактора к реакционной смеси.

Для вычисления α₁ воспользуемся критерием Нуссельта, характеризующим конвективный теплообмен между жидкостью и поверхностью твердого тела:

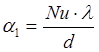, (2.18)

где λ – коэффициент теплопроводности теплоносителя;

d – определяющий размер.

Здесь в качестве определяющего размера необходимо принять эквивалентный диаметр трубы, обладающей таким же сечением, что и пространство внутри рубашки. Внутренний диаметр реактора 0.8 м, наружный – 0.9 м, толщина стенок рубашки и реактора – 0.006 м. Вычислив площадь кольца, найдем диаметр эквивалентной трубы: d =0.36 м. Коэффициент теплопроводности воды λ = 65.9 Вт/(м² · K) . Для нахождения критерия Nu определим характер течения жидкости в рубашке. Это можно сделать, рассчитав критерий Рейнольдса по формуле:

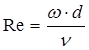, (2.19)

где ω – линейная скорость движения жидкости в трубе;

d – определяющий размер;

ν – кинематическая вязкость среды.

Приняв расход воды 1.5· 10^-4 м³ /с, диаметр подводящей трубы 20 мм, рассчитаем линейную скорость воды в рубашке при максимальном напоре: ω = 0.5 м/с. Кинематическую вязкость при температуре 80 °С примем равной 0.478· 10^-6 м² /с. Из (2.19) получаем Re = 14000. Следовательно, режим течения – турбулентный. Поэтому критерий Нуссельта вычисляется по формуле [3, с.160]:

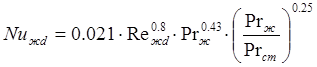. (2.20)

Проведя вычисления по этой формуле, получаем Nu_{ж d} = 89.7. Подставив полученное значение в (2.18), получаем α₁ = 16417 Вт/(м² · K) .

Количественно определить характер движения жидкости в реакторе сложнее, т.к. присутствует мешалка. Можно предположить, что характер движения – турбулентный, обусловленный интенсивным перемешиванием. Среда в реакторе представляет собой сильно разбавленный водный раствор желатины и солей щелочных металлов, поэтому приближенно принимаем условия теплоотдачи от стенки реактора аналогичными условиям теплоотдачи в рубашке и считаем, что α₂ = α₁ = 16000 Вт/(м² · K) .

Второе и третье слагаемые в знаменателе (2.17) равны, т.к. толщина стенок реактора равна толщине стенок рубашки – 6 мм. Стенки рубашки и реактора сделаны из стали 12Х18Н10Т, ее коэффициент теплопроводности λ = 16.88 Вт/(м· K) .