Реферат: Системы стабилизации и ориентации

Т0 - такт квантования.

Описание:

Процедура вычисляет матрицу управления дискретной системы по известной матрице состояния размерности (n´ n), матрице управления размерности (n´m) непрерывной системы и такту квантования по формуле, приведенной в пункте 1.1. Результатом является матрица такой же размерности, что и матрица управления непрерывной системы.

Пример:

diskretB(matrix(2,2,[0,1,2.268,-0.03]),matrix(2,1,[0,-4.235]),0.1);

[ -.4257409375]

[ ]

[.06093613489]

2.2 Получение матрицы передаточных функций

2.2.1 Процедура permatr - получение матрицы передаточных функций.

Формат:

permatr(А,В,с)

Параметры:

А - матрица состояния непрерывной или дискретной системы;

В - матрица управления непрерывной или дискретной системы;

C - строковая переменная s или z, обозначающая передаточную функцию какой системы необходимо вычислить.

Описание:

Процедура вычисляет матрицу передаточных функций дискретной или непрерывной системы n-го порядка согласно пункту 1.2 по формуле (1.7). Результатом выполнения процедуры является матрица n-го порядка, элементами которой являются передаточные функции.

Пример:

permatr(matrix(2,2,[4,3,2,1]),matrix(2,2,[0,1,2,1]),z);

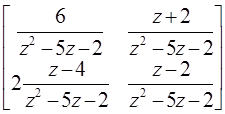
2.3 Построение частотных характеристик

дискретной и непрерывной систем

2.3.1 Процедура afch - построение амплитудно-фазовой частотной характеристики дискретной и непрерывной систем.

Формат:

afch(W,c,Т0)

Параметры:

W - передаточная функция системы;

C - строковая переменная s или z, обозначающая АФЧХ какой системы необходимо построить;

Т0 - такт квантования для дискретной системы.

Описание:

Процедура строит АФЧХ дискретной и непрерывной систем согласно методике, описанной в пункте 1.3.

Пример:

afch(1/(4*s^2-1.8*s+2),s,0.1);

Полученный график можно увидеть на рисунке А.1 приложения А.

2.3.2 Процедура lach - построение логарифмической амплитудно-частотной характеристики дискретной и непрерывной систем.

Формат: