Реферат: Скалярная проекция гиперкомплексных чисел

И для того, чтобы получить проекцию, следует взять действительную часть вектора B’ и провести соответствующую нормировку, поскольку указанным поворотом мы исказили величину модуля вектора B.

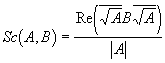
К числу весьма важных свойств скалярного произведения относится:

Поэтому, стремясь найти для гиперкомплексных чисел полную аналогию скалярному произведению, мы не будем использовать нормировок. В этом случае определенное выше правило выглядит как:

И для случая A = B переходит в

Перечислим еще раз свойства скалярного произведения в классическом варианте и найдем соответствия им в случае гиперкомплексных чисел:

1) , причем (x,x) только при x = 0

2) (x,y) = (y,x)

3) (x,ky) = k(x,y) где k - любое действительное число

4) (x,y+z)=(x,y)+(x,z)

Для первого свойства вышеприведенное правило построения проекции не подходит, поскольку

Поскольку даже для тех алгебр, для которых может быть отрицательным числом, число всегда положительно, но исключение составляет условие

(x,x) = 0 только при x = 0

Тут следует сделать оговорку, что в гиперкомплексных алгебрах случай идеалов вовсе не является исключением, поэтому для скалярной проекции гиперкомплексных чисел вполне возможно снять это условие и разрешить

при

Рассмотрим второе свойство скалярного произведения

(x,y) = (y,x)

В случае построения аналогии в нашем случае следует доказать, что

Для этого докажем промежуточные равенства:

a)

b)

Для доказательства равенства a) рассмотрим коэффициенты таблицы произведения мнимых единиц в алгебрах Кэли - Диксона: