Реферат: Случайные величины

3. Из (33.1) следует

,

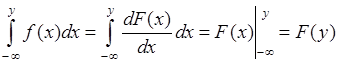поскольку . Таким образом, справедливо равенство

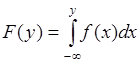. (33.5)

4. Поскольку , то из соотношения (33.5) следует

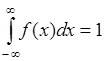(33.6)

- равенство, которое называется условием нормировки. Его левая часть - это вероятность достоверного события.

5. Пусть , тогда из (33.1) следует

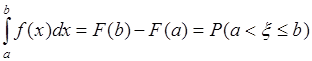. (33.7)

Это соотношение имеет важное значение для приложений, поскольку позволяет вычислить вероятность через плотность вероятности или через функцию распределения вероятностей . Если положить , то из (33.7) следует соотношение (33.6).

На рис. 33.1 представлены примеры графиков функции распределения и плотности вероятностей.

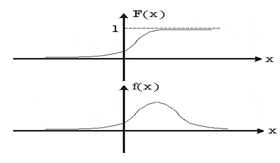
Рис. 33.1. Примеры функции распределения вероятностей и плотности вероятности.

Отметим, что плотность распределения вероятности может иметь несколько максимумов. Значение аргумента , при котором плотность имеет максимум называется модой распределения случайной величины . Если плотность имеет более одной моды, то называется многомодальной.

Плотность распределения вероятностей дискретной случайной величины

Пусть случайная величина принимает значения с вероятностями , . Тогда ее функция распределения вероятностей

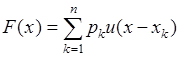, (34.1)

где - функция единичного скачка. Определить плотность вероятности случайной величины по ее функции распределения можно с учетом равенства . Однако при этом возникают математические сложности, связанные с тем, что функция единичного скачка , входящая в (34.1), имеет разрыв первого рода при . Поэтому в точке не существует производная функции .

Для преодоления этой сложности вводится -функция. Функцию единичного скачка можно представить через -функцию следующим равенством:

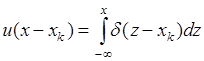. (34.2)

Тогда формально производная

(34.3)

и плотность вероятности дискретной случайной величины определяется из соотношения (34.1) как производная функции :

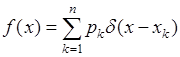. (34.4)

Функция (34.4) обладает всеми свойствами плотности вероятности. Рассмотрим пример. Пусть дискретная случайная величина принимает значения с вероятностями , и пусть , . Тогда вероятность - того, что случайная величина примет значение из отрезка может быть вычислена, исходя из общих свойств плотности по формуле:

.

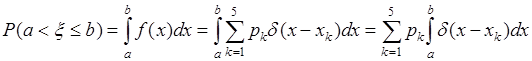Здесь

,

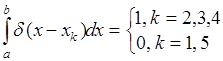поскольку особая точка - функции, определяемая условием , находится внутри области интегрирования при , а при особая точка находится вне области интегрирования. Таким образом,

.
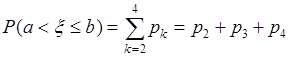