Реферат: Спектральный анализ колебаний

а – нормированный амплитудный спектр; б – фазовый спектр

Распределение энергии в спектре непериодического колебания

Пусть непериодическое колебание описывается функцией . Тогда можно записать

.

Проинтегрируем это выражение по переменной в бесконечных пределах:

В этом выражении

,

где – комплексная величина, сопряженная с .

Следовательно,

.

Произведение двух сопряженных комплексных величин равно квадрату модуля одной из них, поэтому

.

Так как левая часть равенства определяет энергию колебания , то это можно сказать и о правой части. Но тогда

есть ни что иное, как энергия колебания, приходящаяся на один радиан полосы частот для текущей частоты w.

Иными словами, является спектральной плотностью энергии колебания и характеризует распределение энергии в полосе частот колебания:

.

Энергетически значимые участки спектра расположены в тех частотных полосах, в которых значение спектральной плотности относительно велики.

Пример. Определить спектральную плотность энергии прямоугольного видеоимпульса с параметрами: длительность , амплитуда и располагается симметрично относительно начала отсчета времени.

На основании формулы прямого преобразования Фурье найдем спектральную плотность амплитуд

Спектральную плотность энергии легко определить путем возведения в квадрат спектральной плотности амплитуд:

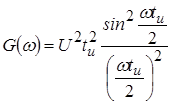
Введем безразмерную переменную и представим результаты определения спектральной плотности амплитуд и спектральной плотности энергии в следующем виде:

;

.

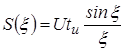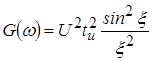Теперь легко построить нормированные спектры как функций безразмерной частотной переменной (рис. 9 и 10).